Question

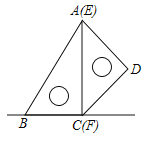
【题目】如图，一副含和角的三角板和拼合在一个平面上，边与重合，.当点从点出发沿方向滑动时，点同时从点出发沿射线方向滑动.当点从点滑动到点时，点运动的路径长为______.

Answer 1

【答案】

【解析】

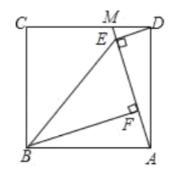
过点D'作D'N⊥AC于点N，作D'M⊥BC于点M，由直角三角形的性质可得BC=4cm，AB=8cm，ED=DF=6cm，由“AAS”可证△D'NE'≌△D'MF'，可得D'N=D'M，即点D'在射线CD上移动，且当E'D'⊥AC时，DD'值最大，则可求点D运动的路径长，

解：∵AC=12cm，∠A=30°，∠DEF=45°

∴BC=4cm，AB=8cm，ED=DF=6cm
如图，当点E沿AC方向下滑时，得△E'D'F'，过点D'作D'N⊥AC于点N，作D'M⊥BC于点M

∴∠MD'N=90°，且∠E'D'F'=90°

∴∠E'D'N=∠F'D'M，且∠D'NE'=∠D'MF'=90°，E'D'=D'F'

∴△D'NE'≌△D'MF'（AAS）

∴D'N=D'M，且D'N⊥AC，D'M⊥CM

∴CD'平分∠ACM

即点E沿AC方向下滑时，点D'在射线CD上移动，

∴当E'D'⊥AC时，DD'值最大，最大值=ED-CD=（12-6）cm
∴当点E从点A滑动到点C时，点D运动的路径长=2×（12-6）=（24-12）cm