题目内容
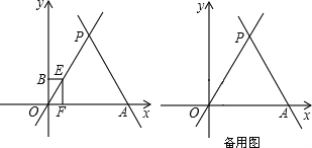
【题目】如图,直线![]() 与x轴相交于点A,与直线
与x轴相交于点A,与直线![]() 相交于点P.
相交于点P.
(1)求点P的坐标.
(2)请判断△OPA的形状并说明理由.
(3)动点E从原点O出发,以每秒1个单位的速度沿着O→P→A的路线向点A匀速运动(E不与点O、A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.求S与t之间的函数关系式.
【答案】(1)![]() ;(2)△POA是等边三角形,理由见解析;(3)当0<t≤4时,
;(2)△POA是等边三角形,理由见解析;(3)当0<t≤4时,![]() ,当4<t<8时,
,当4<t<8时,![]()
【解析】
(1)将两直线的解析式联立组成方程组,解得x、y的值即为两直线的交点坐标的横纵坐标;
(2)求得直线AP与x轴的交点坐标(4,0),利用OP=4PA=4得到OA=OP=PA从而判定△POA是等边三角形;
(3)分别求得OF和EF的值,利用三角形的面积计算方法表示出三角形的面积即可.
解:(1)解方程组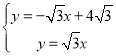 ,
,
解得: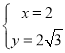 .
.
∴点P的坐标为:![]() ;
;
(2)当y=0时,x=4,
∴点A的坐标为(4,0).
∵![]() ,
,
∴OA=OP=PA,
∴△POA是等边三角形;
(3)①当0<t≤4时,如图,在Rt△EOF中,
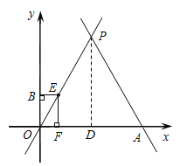
∵∠EOF=60°,OE=t,
∴EF=![]() ,OF=
,OF=![]() ,
,
∴![]() .
.
当4<t<8时,如图,设EB与OP相交于点C,
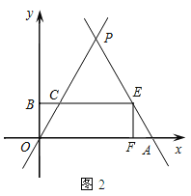
∵CE=PE=t-4,AE=8-t,
∴AF=4-![]() ,EF=
,EF=![]() ,
,
∴OF=OA-AF=4-(4-![]() )=
)=![]() ,
,
∴![]()
=![]() ;
;
综合上述,可得:当0<t≤4时,![]() ;当4<t<8时,
;当4<t<8时,![]() .
.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
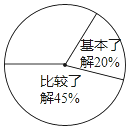
能考试全能100分系列答案【题目】某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了不完整的表格和扇形统计图(如图).
等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
频数 | 50 | m | 40 | 20 |
根据以上提供的信息解答下列问题:
(1)本次问卷调查共抽取的学生数为多少人,表中m的值为多少;
(2)计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数,并补全扇形统计图;
(3)若该校有学生2000人,请根据调查结果估计这些学生中“不太了解”梅山文化知识的人数约为多少?