题目内容
【题目】如图，在四边形ABCD中，AD∥BC，∠ABC+∠DCB=90°，且BC=2AD，分别以AB、BC、DC为边向外作正方形，它们的面积分别为S1、S2、S3．若S2=48，S3=9，则S1的值为（ ）
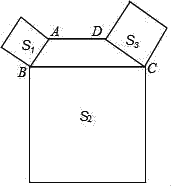
A. 18 B. 12 C. 9 D. 3
【答案】D
【解析】
过A作AH∥CD交BC于H，根据题意得到∠BAE=90°，根据勾股定理计算即可．
∵S2=48，∴BC=4
，过A作AH∥CD交BC于H，则∠AHB=∠DCB．
∵AD∥BC，∴四边形AHCD是平行四边形，∴CH=BH=AD=2，AH=CD=3．
∵∠ABC+∠DCB=90°，∴∠AHB+∠ABC=90°，∴∠BAH=90°，∴AB2=BH2﹣AH2=3，∴S1=3．
故选D．
练习册系列答案
相关题目
