题目内容
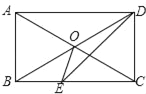
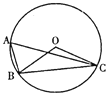
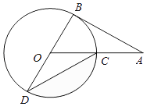
【题目】如图,AB为⊙O的切线,切点为B,连接AO,OA与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为4,则图中阴影部分的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
过O点作OE⊥CD于E,首先根据切线的性质和直角三角形的性质可得∠AOB=60°,再根据平角的定义和三角形外角的性质可得∠COD=120°,∠OCD=∠ODC=30°,根据含30°的直角三角形的性质可得OE,CD的长,再根据阴影部分的面积=扇形OCD的面积-三角形OCD的面积,列式计算即可求解.
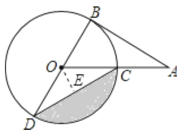
解:如图,过O点作OE⊥CD于E,
∵AB为⊙O的切线,
∴∠ABO=90°,
∵∠A=30°,
∴∠AOB=60°,
∴∠COD=120°,∠OCD=∠ODC=30°,
∴OE=![]() OD=2,CE=DE=
OD=2,CE=DE=![]() OD=2
OD=2![]() ,
,
∴CD=2CE=4![]() ,
,
∴S阴影=S扇形COD-S△COD=![]() -
-![]() ×4
×4![]() ×2=
×2=![]() -4
-4![]() ,
,
故选D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某商场,为了吸引顾客,在“白色情人节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 18 | 24 | 18 |
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.
(2)如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼品券,请你帮助分析选择哪种方案较为实惠.