题目内容
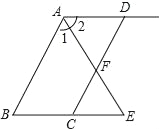
【题目】如图所示,在正方形![]() 中,
中, ![]() 是
是![]() 的中点,
的中点, ![]() 是
是![]() 上一点,且
上一点,且![]() .求证:
.求证: ![]() .
.
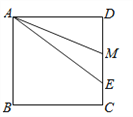
【答案】证明见解析.
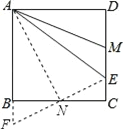
【解析】延长AB到F,使BF=CE,连接EF与BC相交于点N,利用“角角边”证明△BFN和△CEN全等,根据全等三角形对应边相等可得BN=CN,EN=FN,再根据正方形的性质可得∠BAN=∠DAM,然后求出∠BAN=∠EAN,再根据等腰三角形三线合一可得AE=AF,从而得证.
证明:如图,延长AB到F,使BF=CE,连接EF与BC相交于点N,
在△BFN和△CEN中,
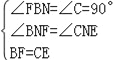 ,
,
∴△BFN≌△CEN(AAS),
∴BN=CN,EN=FN,
又∵M是CD的中点,
∴∠BAN=∠DAM,
∵∠BAE=2∠DAM,
∴∠BAN=∠EAN,
∴AN既是△AEF的角平分线也是中线,
∴AE=AF,
∵AF=AB+BF,
∴AE=BC+CE.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目