Question

【题目】如图，在中，平分，过点作，交于点，交于点，作的平分线交于点，交于点，若，下列结论：①；②；③；④；⑤．其中正确的个数是（ ）

A.2B.3C.4D.5

Answer 1

【答案】C

【解析】

先根据两条角平分线和∠B的度数，得出∠APC的度数，随后即可得出∠PCD的度数，即可判断①正确；

根据角的等量转换得出，然后根据已知可得出∠BAD+∠BCP的度数，即可得出∠AFC+∠DCG的和，即可判断②正确；

由题目中的已知条件无法证明③；

在上截取一点H，使AH=AF，然后根据已知条件，证明和，从而得到，即可得到所求，即④正确；

作PM⊥AB于M，PN⊥AC于N，PQ⊥BC于Q，根据角平分线的性质可得PM=PN=PQ，然后即可推出，则⑤正确．

解析：①∵AD平分∠BAC，CF平分∠ACB，∠B=60°，

∴，

，

∴，故①正确；

②∵CF平分∠ACB，AD平分∠BAC，

∴

∵

∴

，故②正确；

③由题目中的已知条件无法证明BG=AE，故③错误；

④在上截取一点H，使AH=AF

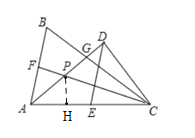
∵AD为∠BAC的角平分线

∴∠BAD=∠CAD

∴

由②知

∴

∴

∴

∴，

∴，故④正确；

⑤作PM⊥AB于M，PN⊥AC于N，PQ⊥BC于Q，

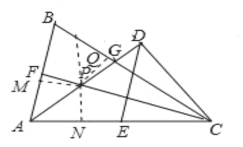
则PM=PN=PQ，

∵S△APF=AF×PM，S△CPG=CG×PQ，S△APC=AC×PN，

∴S△APF+S△CPG=S△APC，故⑤正确；

故选：C．