题目内容
【题目】如图，在△ABC中，点D，E分别为AB，AC的中点，则△ADE与四边形BCED的面积比为（ ）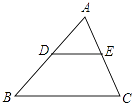
A.1：1
B.1：2
C.1：3
D.1：4
【答案】C
【解析】∵D、E分别为△ABC的边AB、AC上的中点，
∴DE是△ABC的中位线，
∴DE∥BC，DE= 
BC，
∴△ADE∽△ABC，
∴△ADE的面积：△ABC的面积=（ ）2=1：4，
∴△ADE的面积：四边形BCED的面积=1：3；
所以答案是：C．
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识，掌握连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半，以及对相似三角形的判定与性质的理解，了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．
练习册系列答案
相关题目
【题目】为了帮助本市一名患“白血病”的高中生，某班15名同学积极捐款，他们捐款数额如下表：
捐款的数额（单位：元） | 5 | 10 | 20 | 50 | 100 |
人数（单位：个） | 2 | 4 | 5 | 3 | 1 |
关于这15名同学所捐款的数额，下列说法正确的是
A.众数是100 B.平均数是30 C.极差是20 D.中位数是20
【题目】在我校“书香校园”活动中，某数学小组为了解学生家庭藏书情况，随机抽取我校部分学生进行调查，并绘制成部分统计图如下表：
类别 | 家庭藏书情况统计表 | 学生人数 |
|
| 20 |
|
|
|
|
| 50 |
|
| 66 |
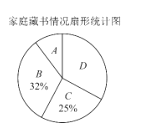
根据以上信息，解答下列问题：
（1）参加调查的学生人数为多少，a等于多少，本次调查结果的中位数在哪一类.
（2）在扇形统计图中，“
”对应扇形的圆心角为多少.
（3）若我校有4500名学生，请估计全校学生中藏书200本以上的人数.
