题目内容
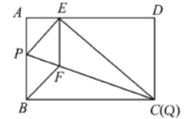
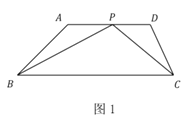
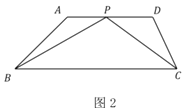
【题目】问题背景:如图,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为边
为边![]() 上一动点,连接
上一动点,连接![]() 、
、![]() .
.
问题探究
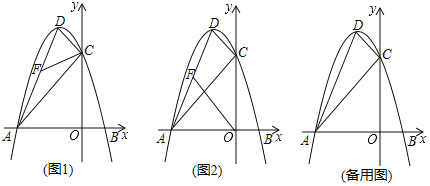
(1)如图1,若![]() ,则
,则![]() 的长为__________.
的长为__________.
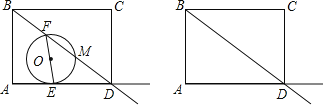
(2)如图2,请求出![]() 周长的最小值;
周长的最小值;
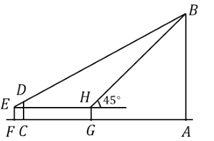
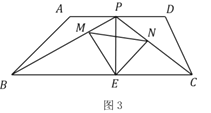
(3)如图3,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 分别作
分别作![]() 于
于![]() ,
,![]() 于点
于点![]() ,连接
,连接![]()
①是否存在点![]() ,使得
,使得![]() 的面积最大?若存在,求出
的面积最大?若存在,求出![]() 面积的最大值,若不存在,请说明理由;
面积的最大值,若不存在,请说明理由;
②请直接写出![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() ;(2)18;(3)①
;(2)18;(3)①![]() ;②
;②![]()
【解析】
(1)过点B作BF⊥AD,交DA的延长线于点F,利用等腰直角三角形ABF求得AF和BF的长,再利用Rt△PBF求得PF的长,进而得解;
(2)作点B关于直线AD的对称点B',连接B'C,交AD于点P',连接BP',根据两点之间线段最短可知当B',P,C三点共线时,![]() 周长取得最小值,再利用勾股定理计算即可;
周长取得最小值,再利用勾股定理计算即可;
(3)①②根据![]() ,
,![]() 可得点E、M、P、N在以PE为直径的圆上,利用圆周角定理和直角三角形两锐角互余可证得△MPN∽△CPB,进而可知当MN最大时,
可得点E、M、P、N在以PE为直径的圆上,利用圆周角定理和直角三角形两锐角互余可证得△MPN∽△CPB,进而可知当MN最大时,![]() 面积的最大,当MN最小时,
面积的最大,当MN最小时,![]() 面积的最小,由圆的性质可知当MN为直径时MN最大,当MN⊥PE时,MN最小,最后利用勾股定理、等积法和相似三角形的性质求解即可.
面积的最小,由圆的性质可知当MN为直径时MN最大,当MN⊥PE时,MN最小,最后利用勾股定理、等积法和相似三角形的性质求解即可.
解:(1)如图,过点B作BF⊥AD,交DA的延长线于点F,
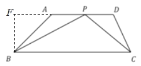
∵AD∥BC,∠ABC=45°,
∴∠FAB=∠ABC=45°,
∵BF⊥AD,
∴在Rt△ABF中,AF2+BF2=AB2,
∵![]()
∴AF=BF=![]() AB=
AB=![]() ,
,
∵AD∥BC,∠PBC=30°,
∴∠FPB=∠PBC=30°,
∵在Rt△PBF中,tan∠FPB=![]()
∴tan30°=![]() ,
,
∴![]()
∴![]() ;
;
(2)如图,作点B关于直线AD的对称点B',连接B'C,交AD于点P',连接BP',
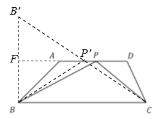
∵点B与点B'关于直线AD对称,
∴AD垂直平分BB',BF=B'F=3,
∴P'B=P'B',BB'=6,
∴当点P在点P'时,PB+PC取得最小值,最小值为B'C的长,此时△BPC的周长最小,
在Rt△BB'C中,B'C=![]() ,
,
∴△BPC的周长最小值为B'C+BC=10+8=18;
(3)①∵![]() ,
,![]() ,
,
∴∠EMP=∠ENP=90°,
∴点E、M、P、N在以PE为直径的圆上,如图所示,
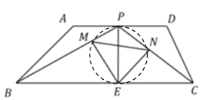
则∠PMN=∠PEN,
∵![]() ,
,![]() ,
,
∴∠PEC=∠ENC=90°,
∴∠PEN+∠NEC =∠NEC+∠PCB=90°,
∴∠PEN =∠PCB,
∴∠PMN=∠PCB,
又∵∠MPN=∠CPB,
∴△MPN∽△CPB,
∴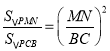
∵![]() ,
,
∴PE=3,
∴![]()
∴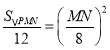
∴当MN取得最大值时,![]() 的面积取得最大值,
的面积取得最大值,
当MN=PE=3时,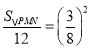 解得
解得![]()
即当MN=PE=3时,![]() 的面积最大,最大值为
的面积最大,最大值为![]() ;
;
②由①可知,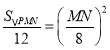 ,
,
∴当MN取得最小值时,![]() 的面积取得最小值,
的面积取得最小值,
由垂径定理可知,当MN⊥PE时,MN取得最小值,
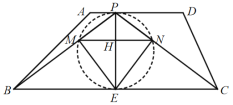
如图,当MN⊥PE时,则弧ME=弧NE
∴∠MPE=∠NPE,
∵![]() ,
,
∴∠PEB=∠PEC=90°,
∴△PEB≌△PEC,
∴EB=EC=![]() BC=4,
BC=4,
在Rt△BEP中,BP=![]() ,
,
∵![]()
∴![]()
∴![]() ,
,
在Rt△PME中,PM=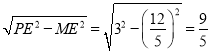
∵![]()
∴![]()
∴![]() ,
,
∴![]() ,
,
∴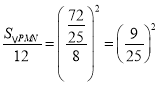 ,
,
解得![]() ,
,
∴![]() 面积的最小值为
面积的最小值为![]() .
.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案【题目】为了传承中华优秀传统文化,某校组织八年级学生参加了“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,绘制如下不完整的条形统计图.
汉字听写大赛成绩分数段统计表
分数段 | 频数 |
| 2 |
| 6 |
| 9 |
| 18 |
| 15 |
汉字听写大赛成绩分数段条形统计图

(1)补全条形统计图.
(2)这次抽取的学生成绩的中位数在________的分数段中;这次抽取的学生成绩在![]() 的分数段的人数占抽取人数的百分比是_______.
的分数段的人数占抽取人数的百分比是_______.
(3)若该校八年级一共有学生350名,成绩在90分以上(含90分)为“优”,则八年级参加这次比赛的学生中成绩“优”等的约有多少人?