题目内容
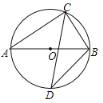
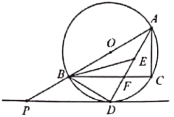
【题目】如图,![]() 内接于以
内接于以![]() 为直径的
为直径的![]() 中,且点
中,且点![]() 是
是![]() 的内心,
的内心,![]() 的延长线与
的延长线与![]() 交于点
交于点![]() ,与
,与![]() 交于点
交于点![]() ,
,![]() 的切线
的切线![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)试判断![]() 的形状,并给予证明;
的形状,并给予证明;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)![]() 是等腰直角三角形,证明见解析;(2)AE=
是等腰直角三角形,证明见解析;(2)AE=![]() .
.
【解析】
(1)根据圆周角定理的推论可得∠BDA=90°,∠ACB=90°,然后根据内心的性质结合三角形外角的性质求出∠BED=45°即可得到![]() 是等腰直角三角形;
是等腰直角三角形;
(2)根据切线的性质求出∠POD=60°,可得∠OAD=30°,然后解等腰直角三角形求出BD=DE=![]() ,进而求出AD=
,进而求出AD=![]() 即可.
即可.
解:(1)![]() 是等腰直角三角形;
是等腰直角三角形;
证明:∵AB是直径,
∴∠BDA=90°,∠ACB=90°,
∴∠CAB+∠CBA=90°,
∵点![]() 是
是![]() 的内心,
的内心,
∴AE,BE分别是∠CAB和∠CBA的角平分线,
∴∠BED=∠BAE+∠ABE=![]() ∠CAB+
∠CAB+![]() ∠CBA=
∠CBA=![]() (∠CAB+∠CBA)=45°,
(∠CAB+∠CBA)=45°,
∴![]() 是等腰直角三角形;
是等腰直角三角形;
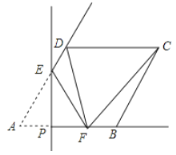
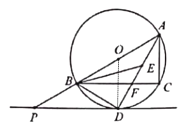
(2)连接OD,
∵![]() 是
是![]() 的切线,
的切线,
∴∠ODP=90°,
∴∠POD=90°-30°=60°,
∵OD=OA,
∴∠OAD=∠ODA=30°,
∵![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,
∴BD=DE=BE·cos45°=2×![]() ,
,
∴AD=![]() ,
,
∴AE=AD-DE=![]() .
.

 智趣寒假作业云南科技出版社系列答案
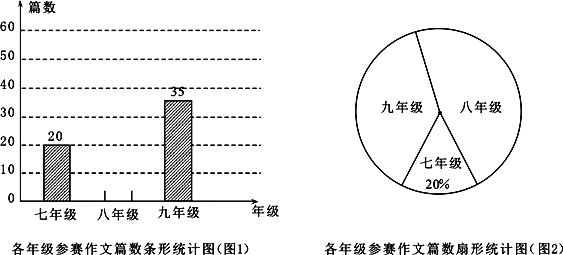
智趣寒假作业云南科技出版社系列答案【题目】为了传承中华优秀传统文化,某校组织八年级学生参加了“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解大赛的成绩分布情况,随机抽取了其中若干名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,绘制如下不完整的条形统计图.
汉字听写大赛成绩分数段统计表
分数段 | 频数 |
| 2 |
| 6 |
| 9 |
| 18 |
| 15 |
汉字听写大赛成绩分数段条形统计图

(1)补全条形统计图.
(2)这次抽取的学生成绩的中位数在________的分数段中;这次抽取的学生成绩在![]() 的分数段的人数占抽取人数的百分比是_______.
的分数段的人数占抽取人数的百分比是_______.
(3)若该校八年级一共有学生350名,成绩在90分以上(含90分)为“优”,则八年级参加这次比赛的学生中成绩“优”等的约有多少人?