题目内容
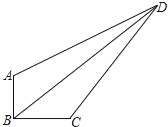
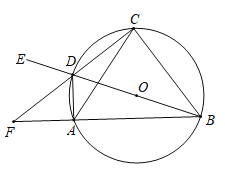
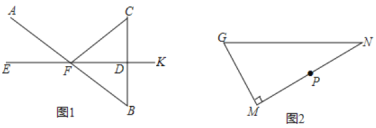
【题目】(1)如图1,已知![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() .
.
求证:![]() .
.
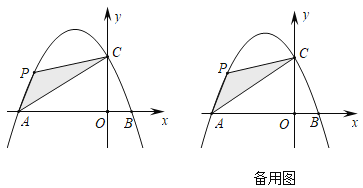
(2)如图2,在![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点.
的中点.
①用直尺和圆规在![]() 边上求作点
边上求作点![]() ,使得
,使得![]() (保留作图痕迹,不要求写作法);
(保留作图痕迹,不要求写作法);
②在①的条件下,如果![]() ,
,![]() ,P为MN中点,求MQ的长度.
,P为MN中点,求MQ的长度.
【答案】(1)见解析;(2)①作点![]() 关于
关于![]() 的对称点
的对称点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,点
,点![]() 即为所求.理由见解析;②MQ=3 .
即为所求.理由见解析;②MQ=3 .
【解析】
(1)证明FC=FB,利用等腰三角形的三线合一的性质即可解决问题.
(2)①作点P关于GN的对称点P′,连P′M交GN于Q,连接PQ,点Q即为所求.
②想办法证明GQ=GN即可.
(1)证明:如图1中,
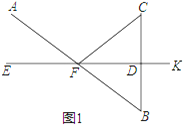
![]() 垂直平分线段
垂直平分线段![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
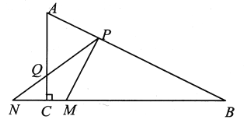
(2)①作点![]() 关于
关于![]() 的对称点
的对称点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,点
,点![]() 即为所求.
即为所求.
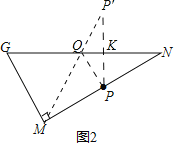
理由:![]() 垂直平分
垂直平分![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 点
点![]() 即为所求.
即为所求.
②∵P,P′关于GN对称,
∴GN⊥PP′,PK=KP′,
∴∠PKN=90°,
∵∠N=30°,
∴∠PNK=60°,
∴PN=2KP=PP′,
∵PM=PN,
∴PM=PP′,
∵∠NPK=∠PMP′+∠P′,
∴∠PMP′=∠P′=30°,
∴∠QMN=∠N=30°,
∴MQ=NQ,
∵∠G=∠QMG=60°,
∴QG=QM,
∴MQ=QG=NQ,
∵GM=3,∠N=30°,∠NMG=90°,
∴GN=2GM=6,
∴MQ=3.

练习册系列答案
相关题目