题目内容
【题目】如图1，点P为∠MON的平分线上一点，以P为顶点的角的两边分别与射线OM，ON交于A，B两点，如果∠APB绕点P旋转时始终满足OAOB=OP2 ， 我们就把∠APB叫做∠MON的智慧角．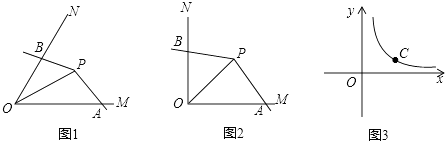
（1）如图2，已知∠MON=90°，点P为∠MON的平分线上一点，以P为顶点的角的两边分别与射线OM，ON交于A，B两点，且∠APB=135°．求证：∠APB是∠MON的智慧角．
（2）如图1，已知∠MON=α（0°＜α＜90°），OP=2．若∠APB是∠MON的智慧角，连结AB，用含α的式子分别表示∠APB的度数和△AOB的面积．
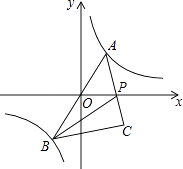
（3）如图3，C是函数y= 
（x＞0）图象上的一个动点，过C的直线CD分别交x轴和y轴于A，B两点，且满足BC=2CA，请求出∠AOB的智慧角∠APB的顶点P的坐标．
【答案】
（1）
证明：∵∠MON=90°，P为∠MON的平分线上一点，
∴∠AOP=∠BOP= 
∠MON=45°，
∵∠AOP+∠OAP+∠APO=180°，
∴∠OAP+∠APO=135°，
∵∠APB=135°，
∴∠APO+∠OPB=135°，
∴∠OAP=∠OPB，
∴△AOP∽△POB，
∴ 
，
∴OP2=OAOB，
∴∠APB是∠MON的智慧角
（2）
解：∵∠APB是∠MON的智慧角，
∴OAOB=OP2，
∴ ，
∵P为∠MON的平分线上一点，
∴∠AOP=∠BOP= α，
∴△AOP∽△POB，
∴∠OAP=∠OPB，
∴∠APB=∠OPB+∠OPA=∠OAP+∠OPA=180°﹣ α，
即∠APB=180°﹣ α；
过点A作AH⊥OB于H，连接AB；如图1所示：
则S△AOB= OBAH= OBOAsinα= OP2sinα，
∵OP=2，
∴S△AOB=2sinα；
（3）
设点C（a，b），则ab=3，过点C作CH⊥OA于H；分两种情况：
①当点B在y轴正半轴上时；当点A在x轴的负半轴上时，如图2所示：
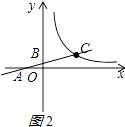
BC=2CA不可能；
当点A在x轴的正半轴上时，如图3所示：
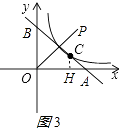
∵BC=2CA，
∴ 
，
∵CH∥OB，
∴△ACH∽△ABO，
∴ 
= 
，
∴OB=3b，OA= 
，
∴OAOB= 3b= 
= 
，
∵∠APB是∠AOB的智慧角，
∴OP= 
= 
= 
，
∵∠AOB=90°，OP平分∠AOB，
∴点P的坐标为：（ 
， ）；
②当点B在y轴的负半轴上时，如图4所示：
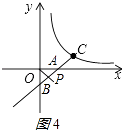
∵BC=2CA，
∴AB=CA，
在△ACH和△ABO中，
，
∴△ACH≌△ABO（AAS），
∴OB=CH=b，OA=AH= a，
∴OAOB= ab= 
，
∵∠APB是∠AOB的智慧角，
∴OP= = 
= 
，
∵∠AOB=90°，OP平分∠AOB，
∴点P的坐标为：（ 
，﹣ ）；
综上所述：点P的坐标为：（ ， ），或（ ，﹣ ）．
【解析】（1）由角平分线求出∠AOP=∠BOP= ∠MON=45°，再证出∠OAP=∠OPB，证明△AOP∽△POB，得出对应边成比例 ，得出OP2=OAOB，即可得出结论；（2）由∠APB是∠MON的智慧角，得出 ，证出△AOP∽△POB，得出对应角相等∠OAP=∠OPB，即可得出∠APB=180°﹣ α；过点A作AH⊥OB于H，由三角形的面积公式得出：S△AOB= OBAH，即可得出S△AOB=2sinα；（3）设点C（a，b），则ab=3，过点C作CH⊥OA于H；分两种情况：
①当点B在y轴正半轴上时；当点A在x轴的负半轴上时，BC=2CA不可能；当得A在x轴的正半轴上时；先求出 ，由平行线得出△ACH∽△ABO，得出比例式： 
= ，得出OB=3b，OA= ，求出OAOB= ，根据∠APB是∠AOB的智慧角，得出OP，即可得出点P的坐标；
②当点B在y轴的负半轴上时；由题意得出：AB=CA，由AAS证明△ACH≌△ABO，得出OB=CH=b，OA=AH= a，得出OAOB= ，求出OP，即可得出点P的坐标．
【考点精析】本题主要考查了反比例函数的性质的相关知识点，需要掌握性质:当k＞0时双曲线的两支分别位于第一、第三象限，在每个象限内y值随x值的增大而减小； 当k＜0时双曲线的两支分别位于第二、第四象限，在每个象限内y值随x值的增大而增大才能正确解答此题．
