Question

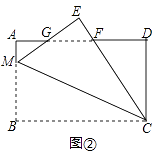
【题目】如图，在等腰△ABC中，点D、E分别是两腰AC、BC上的点，连接AE、BD相交于点O，∠1=∠2．
（1）求证：OD=OE；
（2）求证：四边形ABED是等腰梯形；
（3）若AB=3DE，△DCE的面积为2，求四边形ABED的面积．

Answer 1

【答案】
（1）证明：如图，∵△ABC是等腰三角形，

∴AC=BC，

∴∠BAD=∠ABE，

又∵AB=BA、∠2=∠1，

∴△ABD≌△BAE（ASA），

∴BD=AE，

又∵∠1=∠2，

∴OA=OB，

∴BD﹣OB=AE﹣OA，

即：OD=OE

（2）证明：由①得OD=OE，

∴∠DOE=∠BOA，

，

∴△DOE∽△BOA，

∴∠EDO=∠ABO，

∴DE∥AB，

又∵∠DAB=∠EBA，

∴四边形ABEO为等腰梯形

（3）解：由（2）可知：DE∥AB，

∴∠CED=∠CBA，∠CDE=∠CAB，

∴△DCE∽△ACB（AA），

∴ =（ ）2，

即 =（ ）2= ．

∴S△ACB=18，

∴S四边形ABED=S△ACB﹣S△DCE=18﹣2=16

【解析】（1）如图，由△ABC是等腰三角形，得到∠BAD=∠ABE，然后利用已知条件证明△ABD≌△BAE，由全等三角形的性质得到BD=AE，又由∠1=∠2得到OA=OB，由此即可证明OD=OE；（2）由（1）得OD=OE根据等腰三角形的性质得到∠OED=∠ODE，根据三角形的内角和得到∠OED= （180°﹣∠DOE），∠1= （180°﹣∠AOB），而∠DOE=∠AOB，所以得到∠1=∠OED，然后利用平行线的判定得到DE∥AB，最后证明AD与BE不平行，这样就可以证明梯形ABED是等腰梯形；（3）由（2）可知DE∥AB，然后得到△DCE∽△ACB，接着利用相似三角形的性质即可求出S△ACB ， 然后就可以求出S四边形ABED ．
【考点精析】通过灵活运用等腰三角形的性质和等腰梯形的判定，掌握等腰三角形的两个底角相等（简称：等边对等角）；两腰相等的梯形是等腰梯形；同一底上的两个角相等的梯形是等腰梯形；两条对角线相等的梯形是等腰梯形即可以解答此题．