题目内容
【题目】问题背景
已知在△ABC中，AB边上的动点D由A向B运动（与A，B不重合），点E与点D同时出发，由点C沿BC的延长线方向运动（E不与C重合），连接DE交AC于点F，点H是线段AF上一点．
（1）初步尝试
如图1，若△ABC是等边三角形，DH⊥AC，且点D，E的运动速度相等．
求证：HF=AH+CF．
小五同学发现可以由以下两种思路解决此问题：
思路一：过点D作DG∥BC，交AC于点G，先证GH=AH，再证GF=CF，从而证得结论成立；
思路二：过点E作EM⊥AC，交AC的延长线于点M，先证CM=AH，再证HF=MF，从而证得结论成立．
请你任选一种思路，完整地书写本小题的证明过程（如用两种方法作答，则以第一种方法评分）；
（2）类比探究
如图2，若在△ABC中，∠ABC=90°，∠ADH=∠BAC=30°，且D，E的运动速度之比是 
：1，求 
的值；
（3）延伸拓展
如图3，若在△ABC中，AB=AC，∠ADH=∠BAC=36°，记 
=m，且点D，E运动速度相等，试用含m的代数式表示 （直接写出结果，不必写解答过程）．
【答案】
（1）
证明（选择思路一）：过点D作DG∥BC，交AC于点G，如图1所示：
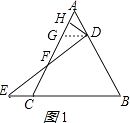
则∠ADG=∠B，∠AGD=∠ACB，
∵△ABC是等边三角形，
∴∠A=∠B=∠ACB=60°，
∴∠ADG=∠AGD=∠A，
∴△ADG是等边三角形，
∴GD=AD=CE，
∵DH⊥AC，
∴GH=AH，
∵DG∥BC，
∴∠GDF=∠CEF，∠DGF=∠ECF，
在△GDF和△CEF中，
，
∴△GDF≌△CEF（ASA），
∴GF=CF，
∴GH+GF=AH+CF，
即HF=AH+CF
（2）
解：过点D作DG∥BC，交AC于点G，如图2所示：
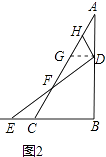
则∠ADG=∠B=90°，
∵∠BAC=∠ADH=30°，
∴∠HGD=∠HDG=60°，
∴AH=GH=GD，AD= 
GD，
根据题意得：AD= CE，
∴GD=CE，
∵DG∥BC，
∴∠GDF=∠CEF，∠DGF=∠ECF，
在△GDF和△CEF中，
，
∴△GDF≌△CEF（ASA），
∴GF=CF，
∴GH+GF=AH+CF，
即HF=AH+CF，
∴ 
=2；
（3）
解： 
，理由如下：
过点D作DG∥BC，交AC于点G，如图3所示：
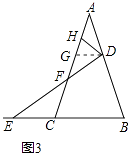
则∠ADG=∠B，∠AGD=∠ACB，
∵AB=AC，∠BAC=36°，
∴∠ACB=∠B=∠ADG=∠AGD=72°，
∵∠ADH=∠BAC=36°，
∴AH=DH，∠DHG=72°=∠AGD，
∴DG=DH=AH，△ADG∽△ABC，△ADG∽△DGH，
∴ 
=m， 
=m，
∴△DGH∽△ABC，
∴ 
=m，
∴ 
=m，
∵DG∥BC，
∴△DFG∽△EFC，
∴ 
=m，
∴ 
=m，
即 
=m，
∴ 
= 
，
∴ = 
= 
= 
．
【解析】（1）过点D作DG∥BC，交AC于点G，先证明△ADG是等边三角形，得出GD=AD=CE，再证明GH=AH，由ASA证明△GDF≌△CEF，得出GF=CF，即可得出结论；（2）过点D作DG∥BC，交AC于点G，先证出AH=GH=GD，AD= GD，由题意AD= CE，得出GD=CE，再证明△GDF≌△CEF，得出GF=CF，即可得出结论；（3）过点D作DG∥BC，交AC于点G，先证出 DG=DH=AH，再证明△ADG∽△ABC，△ADG∽△DGH，△DGH∽△ABC，得出 =m， =m，△DGH∽△ABC，得出 =m， =m，证明△DFG∽△EFC，得出 =m， =m， = ，即可得出结果．
【考点精析】解答此题的关键在于理解相似三角形的应用的相关知识，掌握测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解．
