Question

【题目】如图，在矩形ABCD中，AB=8，AD=12，过A，D两点的⊙O与BC边相切于点E，则⊙O的半径为 ．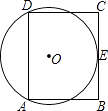

Answer 1

【答案】6.25
【解析】解：连接OE，并反向延长交AD于点F，连接OA，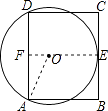
∵BC是切线，
∴OE⊥BC，
∴∠OEC=90°，
∵四边形ABCD是矩形，
∴∠C=∠D=90°，
∴四边形CDFE是矩形，
∴EF=CD=AB=8，OF⊥AD，
∴AF= AD= ×12=6，
设⊙O的半径为x，则OF=EF﹣OE=8﹣x，
在Rt△OAF中，OF2+AF2=OA2 ，
则（8﹣x）2+36=x2 ，
解得：x=6.25，
∴⊙O的半径为：6.25．
故答案为：6.25．
首先连接OE，并反向延长交AD于点F，连接OA，由在矩形ABCD中，过A，D两点的⊙O与BC边相切于点E，易得四边形CDFE是矩形，由垂径定理可求得AF的长，然后设⊙O的半径为x，则OE=EF﹣OE=8﹣x，利用勾股定理即可得：（8﹣x）2+36=x2 ， 继而求得答案．