题目内容
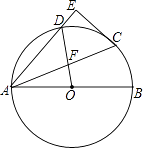
【题目】如图AB是⊙O的直径,∠A=30°,延长OB到D使BD=OB. 
(1)△OBC是否是等边三角形?说明理由;
(2)求证:DC是⊙O的切线.
【答案】
(1)解:△OBC是等边三角形.理由如下:
∵∠A=30°,
∴∠BOC=60°,
∵OB=OC,
∴△OBC是等边三角形
(2)证明:∵BD=OB,△OBC是等边三角形.
∴∠OCB=∠OBC=60°,BD=BC.
∴∠BCD=30°.
∴∠OCD=90°.
∴DC是⊙O的切线
【解析】(1)根据同弧所对的圆周角等于它所对的圆心角的一半,可知∠BOC=60°,又OB=OC,依此可以证明△OBC是否是等边三角形.(2)要证PC是⊙O的切线,只要证明∠DCO=90°即可.
【考点精析】根据题目的已知条件,利用等边三角形的判定和圆周角定理的相关知识可以得到问题的答案,需要掌握三个角都相等的三角形是等边三角形;有一个角等于60°的等腰三角形是等边三角形;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

练习册系列答案
相关题目