题目内容
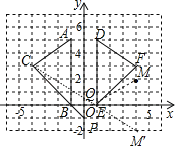
【题目】如图,在平面直角坐标系中,A(﹣1,5)、B(﹣1,0)、C(﹣4,3).

(1)请画出△ABC关于y轴对称的△DEF(其中D、E、F分别是A、B、C的对应点).
(2)直接写出(1)中F点的坐标为 .
(3)若直线l经过点(0,﹣2)且与x轴平行,则点C关于直线l的对称点的坐标为 .
(4)在y轴上存在一点P,使PC﹣PB最大,则点P的坐标为 .
(5)第一象限有一点M(4,2),在x轴上找一点Q使CQ+MQ最短,画出最短路径,保留作图痕迹.
【答案】(1)见解析;(2)点F的坐标(4,3);(3)点C关于直线l的对称点C′(﹣4,﹣9);(4)(0,﹣1);(5)见解析.
【解析】
(1)分别作出A,B,C的对应点D,E,F即可.
(2)根据点F的位置写出坐标即可.
(3)根据对称的性质解决问题即可.
(4)延长CB交y轴于点P,此时PC﹣PB的值最大.
(5)作点M关于x轴的对称点M′,连接CM′交x轴于点Q,连接QM,此时QM+QC的值最小.
(1)如图,△DEF即为所求.
(2)点F的坐标(4,3).
故答案为(4,3).
(3)∵C(﹣4,3),直线l为y=﹣2,
∴点C关于直线l的对称点C′(﹣4,﹣9).
(4)延长CB交y轴于点P,此时PC﹣PB的值最大,P(0,﹣1),
故答案为(0,﹣1).
(5)作点M关于x轴的对称点M′,连接CM′交x轴于点Q,连接QM,此时QM+QC的值最小.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目