��Ŀ����
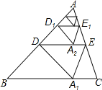
����Ŀ���ڵȱ�������ABC�У���D��BC���е㣬��E��F�ֱ��DZ�AB��AC�����߶�AB��AC�Ķ˵㣩�ϵĶ��㣬�ҡ�EDF��120����С����С�۶����ͼ��չ�������о���
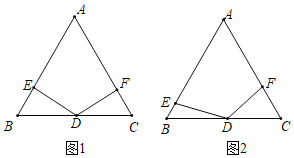
�����̽����1����ͼ1��С�����֣�����DEB��90��ʱ��BE+CF��nAB����n��ֵΪ�� ����
������̽����2����ͼ2���ڵ�E��F���˶������У�С�۷���������Ȥ�Ľ��ۣ�
��DEʼ�յ���DF����BE��CF�ĺ�ʼ�ղ��䣻����ѡ������һ�����ۼ���֤����
�ɹ�����:��3�����߳�AB��8���ڵ�E��F���˶������У����ı���DEAF���ܳ�ΪL��L��DE+EA+AF+FD�����ܳ�L ȡ���ֵ����СֵʱE���λ��?
���𰸡���1��![]() ����2���ټ��������ڼ���������3���ܳ�L ȡ���ֵʱ��E�͵�B�غϻ�BE=4��ȡ��СֵʱBE=2��
����2���ټ��������ڼ���������3���ܳ�L ȡ���ֵʱ��E�͵�B�غϻ�BE=4��ȡ��СֵʱBE=2��
��������
��1�������õȱ��������жϳ�BD=CD=![]() AB�������жϳ�BE=
AB�������жϳ�BE=![]() BD�����жϳ���DFC=90�����ó�CF=
BD�����жϳ���DFC=90�����ó�CF=![]() CD�����ɵó����ۣ�
CD�����ɵó����ۣ�
��2���ٹ������EDG�ա�FDH��ASA�����ó�DE=DF�����ɵó����ۣ�
���ɣ�1��֪��BG+CH=![]() AB���ɢ�֪����EDG�ա�FDH��ASA�����ó�EG=FH�����ɵó����ۣ�
AB���ɢ�֪����EDG�ա�FDH��ASA�����ó�EG=FH�����ɵó����ۣ�
��3���ɣ�1����2���жϳ�L=2DE+12�����жϳ�DE��ABʱ��L��С����F�͵�C�غ�ʱ��DE����ɵó����ۣ�
�⣺��1���ߡ�ABC�ǵȱ������Σ�
���B=��C=60����AB=BC��
�ߵ�D��BC���е㣬
��BD=CD=![]() BC=
BC=![]() AB��
AB��
�ߡ�DEB=90����
���BDE=90��-��B=30����
��Rt��BDE��BE=![]() BD��
BD��
�ߡ�EDF=120������BDE=30����
���CDF=180��-��BDE-��EDF=30����
�ߡ�C=60����
���DFC=90����
��Rt��CFD��CF=![]() CD��
CD��
��BE+CF=![]() BD+
BD+![]() CD=
CD=![]() BC=
BC=![]() AB��
AB��
��BE+CF=nAB��
��n=![]() ��
��
�ʴ�Ϊ��![]() ��
��
��2����ͼ��
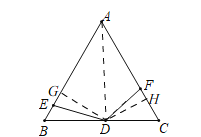
�ٹ���D��DG��AB��G��DH��AC��H��
���DGB=��AGD=��CHD=��AHD=90����
�ߡ�ABC�ǵȱ������Σ�
���A=60����
���GDH=360��-��AGD-��AHD-��A=120����
�ߡ�EDF=120����
���EDG=��FDH��
�ߡ�ABC�ǵȱ������Σ���D��BC���е㣬
���BAD=��CAD��
��DG��AB��DH��AC��
��DG=DH��
�ڡ�EDG�͡�FDH�У�
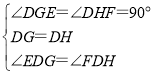 ��
��
���EDG�ա�FDH��ASA����
��DE=DF��
����DEʼ�յ���DF��
��ͬ��1���ķ����ã�BG+CH=![]() AB��
AB��
�ɢ�֪����EDG�ա�FDH��ASA����
��EG=FH��
��BE+CF=BG-EG+CH+FH=BG+CH=![]() AB��
AB��
��BE��CF�ĺ�ʼ�ղ��䣻
��3���ɣ�2��֪��DE=DF��BE+CF=![]() AB��
AB��
��AB=8��
��BE+CF=4��
���ı���DEAF���ܳ�ΪL=DE+EA+AF+FD
=DE+AB-BE+AC-CF+DF
=DE+AB-BE+AB-CF+DE
=2DE+2AB-��BE+CF��
=2DE+2��8-4
=2DE+12��
��DE���ʱ��L���DE��Сʱ��L��С��
��DE��ABʱ��DE��С��L��С��
��ʱ��BDE=90��-60��=30����
BE=![]() BD=2��
BD=2��
����F�͵�C�غϻ��E�͵�B�غ�ʱ��DE���F�͵�C�غ�ʱ����BDE=180��-��EDF=120��=60����
�ߡ�B=60����
���B=��BDE=��BED=60����
���BDE�ǵȱ������Σ�
��BE=DE=BD=![]() AB=4��
AB=4��
����E�͵�B�غ�ʱ��DE=BD=4���ܳ�L �����ֵ��
���ܳ�L ȡ���ֵʱ��E�͵�B�غϻ�BE=4��ȡ��СֵʱBE=2��

 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�����Ŀ�����꼶ij��Ϊ���Ƽ��ڱ��õĽ�Ʒ���ƻ������곬�й���ʼDZ���ˮ�ʹ�40�����ڻ�֪ij����������һ������������Ӹ����깺����Щ��Ʒ����֪�ʼDZ���ˮ�����������̵�����ۼ۷ֱ����±����������곬�й�����Щ��Ʒ�軨��90Ԫ��
Ʒ���̵� | �ʼDZ���Ԫ/���� | ˮ�ʣ�Ԫ/���� |
���곬�� | 2.4 | 2 |
���� | 2 | 1.8 |
��1��������蹺��ʼDZ���ˮ�ʵ�������
��2��������깺����Щ��Ʒ�ɽ�ʡ����Ԫ��