题目内容
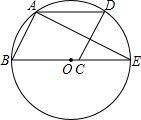
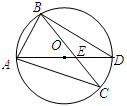
如图,CA、CB为⊙O的切线,切点分别为A、B.直径延长AD与CB的延长线交于点E.AB、CO交于点M,连接OB.
(1)求证:∠ABO=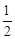 ∠ACB;
∠ACB;
(2)若sin∠EAB=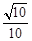 ,CB=12,求⊙O 的半径及
,CB=12,求⊙O 的半径及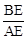 的值.
的值.
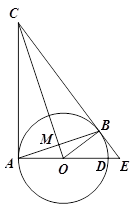
(1)求证:∠ABO=
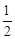 ∠ACB;
∠ACB;(2)若sin∠EAB=
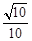 ,CB=12,求⊙O 的半径及
,CB=12,求⊙O 的半径及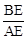 的值.
的值.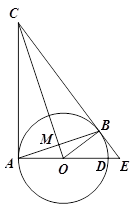
(1)证明见解析;(2)4,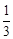 .
.
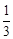 .
.试题分析:(1)证明∠ABO =∠BCO即可证得∠ABO=
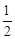 ∠ACB.
∠ACB.(2)由sin∠BCO =sin∠EAB=
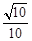 可求得
可求得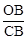 =
=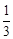 ,从而由CB=12求得⊙O 的半径OB为4;由△OBE∽△CAE列比例式得
,从而由CB=12求得⊙O 的半径OB为4;由△OBE∽△CAE列比例式得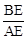 =
=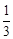 .
.(1)∵CA、CB为⊙O的切线,
∴ CA=CB, ∠BCO=
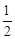 ∠ACB,∴∠CBO=90°.∴ CO⊥AB.
∠ACB,∴∠CBO=90°.∴ CO⊥AB.∴∠ABO +∠CBM=∠BCO +∠CBM=90°.∴∠ABO =∠BCO.∴∠ABO=
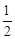 ∠ACB.
∠ACB.(2) ∵ OA=OB, ∴∠EAB=∠ABO.∴∠BCO=∠EAB.
∵ sin∠BCO =sin∠EAB=
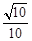 ,∴
,∴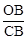 =
=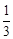 .
.∵ CB=12,∴ OB=4,即⊙O 的半径为4.
∵∠OBE=∠CAE=90°,∠E=∠E,∴△OBE∽△CAE.∴
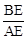 =
=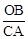 .
.∵CA=CB=12,∴
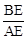 =
=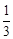 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是恒成立的.
是恒成立的. 恒成立,说明
恒成立,说明

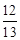 ,cos 67.4°=
,cos 67.4°=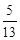 ,tan 67.4° =
,tan 67.4° =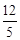 )
)