题目内容
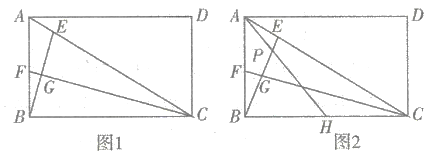
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边的中点,将
边的中点,将![]() 绕
绕![]() 点旋转
点旋转![]() 得到
得到![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有______(只填写序号).
.其中正确的结论有______(只填写序号).
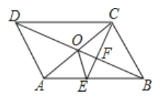
【答案】①②③
【解析】
根据旋转性质、平行线性质证得EC=EA=BC,推出∠DCB=120°,再由角平分线的性质推出∠EBC=∠BCE=∠CEB=60°,推出EA=EB=EC,然后根据中位线定理得出![]() =60°,即可判断结论①正确;由平行线分线段成比例定理得出OB=3OF,S△COB=3S△COF,进而得出结论②正确;由∠ACB=90°,设BC=a, 则AB=2a,AC=
=60°,即可判断结论①正确;由平行线分线段成比例定理得出OB=3OF,S△COB=3S△COF,进而得出结论②正确;由∠ACB=90°,设BC=a, 则AB=2a,AC=![]() a,
a,
OA=OC=![]() a,根据勾股定理得出OD,进而求得结论③正确;根据以上线段的关系用含a的代数式表示:OD=
a,根据勾股定理得出OD,进而求得结论③正确;根据以上线段的关系用含a的代数式表示:OD=![]() ,OF=
,OF=![]() ,FB=
,FB=![]() ,即可求得
,即可求得![]() ,即结论④错误.
,即结论④错误.
解:根据旋转性质可知,OD=OB,OA=OC,∠ACD=∠CAB,
∴CD//AB
∵CD//AB,∠ABC=60°,
∴∠DCB+∠ABC=180°,
∴∠DCB=120°,
∵EC平分∠DCB,
∴∠ECB=∠DCB=60°,
∴∠EBC=∠BCE=∠CEB=60°,△ECB是等边三角形,
∴EB=BC,
∵AB=2BC,
∴EA=EB=EC,
∵OA=OC,
∴OE∥BC
∴∠AEO=∠ABC=60°
∴∠CEO=60°
∴![]()
故结论①正确;
∵OE∥BC,AE=EB
∴2OE=BC
∴2OF=BF
∴OB=3OF∴S△COB=3S△COF
∵S△COB=S△AOD
∴OB=3OF
故结论②正确;
∵AE=EC,∠CEB=60°
∴∠ACE=∠A=30°,
∴∠ACB=90°
设BC=a,则AB=2a,AC=![]() a,
a,
∴OA=OC=![]() a
a
OD=OB=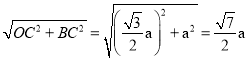
∴![]()
故结论③正确;
∵OD=![]() ,OF=
,OF=![]() ,FB=
,FB=![]()
∴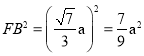
OF·OD=![]()
∴![]()
故结论④不成立
故答案为:①②③

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目