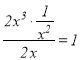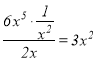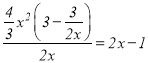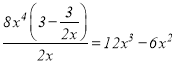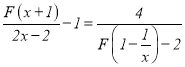题目内容
【题目】在△ABC 中,∠A=30°,∠B=90°,AC=8,点 D 在边 AB, 且 BD=![]() ,点 P 是△ABC 边上的一个动点,若 AP=2PD 时,则 PD的长是____________.
,点 P 是△ABC 边上的一个动点,若 AP=2PD 时,则 PD的长是____________.
【答案】3或![]() 或
或![]()
【解析】
根据直角三角形的性质求出BC,勾股定理求出AB,根据直角三角形的性质列式计算即可.
解:如图

∵∠B=90°,∠A=30°,
∴BC=![]() AC=
AC=![]() ×8=4,
×8=4,
由勾股定理得,AB=![]()
![]()
当点P在AC上时,∠A=30°,AP=2PD,
∴∠ADP=90°,
则AD2+PD2=AP2,即(3![]() )2=(2PD)2-PD2,
)2=(2PD)2-PD2,
解得,PD=3,
当点P在AB上时,AP=2PD,AD=3![]() ,
,
∴PD=![]() ,
,
当点P在BC上时,AP=2PD,
设PD=x,则AP=2x,
由勾股定理得,BP2=PD2-BD2=x2-3,
![]()
解得,x=![]()
故答案为:3或![]() 或
或![]() .
.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目