题目内容
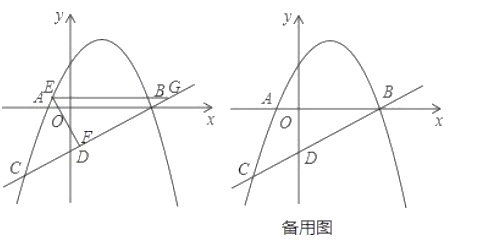
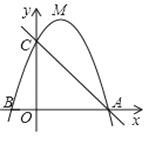
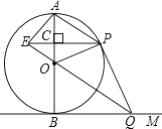
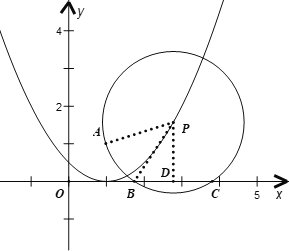
【题目】二次函数y=![]() (x-h)2+k的顶点在x轴上,其对称轴与直线y=x交于点A(1,1),点P是抛物线上一点,以P为圆心,PA长为半径画圆,⊙P交x轴于B、C两点.
(x-h)2+k的顶点在x轴上,其对称轴与直线y=x交于点A(1,1),点P是抛物线上一点,以P为圆心,PA长为半径画圆,⊙P交x轴于B、C两点.
⑴h= ,k= ;
⑵①当点P在顶点时,BC= ;
②BC的值是否随P点横坐标的变化而变化?如果变化,请说明理由,如果不变化,请求出这个值.
【答案】(1)1,0;(2)①2;②BC的值不随P点横坐标的变化而变化,![]() .
.
【解析】
(1)分别求出二次函数的对称轴、顶点的纵坐标即可得;
(2)①根据题(1)可得二次函数的解析式,从而可得顶点坐标,再根据当点P在顶点时,BC恰好为圆P的直径即可得;
②先依据题意画出图形,如图(见解析),先根据垂径定理得出![]() ,再根据点的坐标、两点之间的距离公式分别求出
,再根据点的坐标、两点之间的距离公式分别求出![]() 、
、![]() 的值,然后利用勾股定理求出
的值,然后利用勾股定理求出![]() ,从而可得
,从而可得![]() ,即可得出答案.
,即可得出答案.
(1)由题意得:此二次函数的对称轴为![]() ,顶点的纵坐标为0
,顶点的纵坐标为0
则![]() ,
,![]()
故答案为:1,0;
(2)①由(1)可知,此二次函数的解析式为![]() ,其顶点坐标为
,其顶点坐标为![]()
当点P在顶点时,半径![]()
此时,BC恰好为圆P的直径,即![]()
故答案为:2;
②BC的值不随P点横坐标的变化而变化,求解过程如下:
如图,过点P作![]() 轴于点D,连接PA、PB,则
轴于点D,连接PA、PB,则![]()
由垂径定理得:![]()
设点P的坐标为![]() ,则
,则![]()
由两点之间的公式得:![]()
在![]() 中,
中,![]()
即![]()
解得![]() 或
或![]() (不符题意,舍去)
(不符题意,舍去)
![]()
故BC的值不随P点横坐标的变化而变化,![]() .
.

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案【题目】近年来,共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一,许多高校均投放了使用手机支付就可随取随用的共享单车.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数(次) | 0 | 1 | 2 | 3 | 4 | 5 |
人数(人) | 11 | 15 | 23 | 28 | 20 | 3 |
(1)这天部分出行学生使用共享单车次数的众数是_________(次).
(2)求这天部分出行学生平均每人使用共享单车的次数.
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少人?