ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΒΡΓΑ―νΜ‘»ΐΫ«Γ±ΗφΥΏΝΥΈ“Ο«Εΰœν Ϋ≥ΥΖΫ’ΙΩΣ ΫΒΡœΒ ΐΙφ¬…Θ§»γΘΚΒΎ»ΐ––ΒΡ»ΐΗω ΐΘ®1ΓΔ2ΓΔ1Θ©«ΓΚΟΕ‘”ΠΉ≈Θ®a+bΘ©2ΒΡ’ΙΩΣ Ϋa2+2ab+b2ΒΡœΒ ΐΘΜΒΎΥΡ––ΒΡΥΡΗω ΐ«ΓΚΟΕ‘”ΠΉ≈Θ®a+bΘ©3ΘΫa3+3a2b+3ab2+b3ΒΡœΒ ΐΘ§ΗυΨί ΐ±μ÷–«ΑΈε––ΒΡ ΐΉ÷ΥυΖ¥”≥ΒΡΙφ¬…Θ§ΜΊ¥πΘΚ
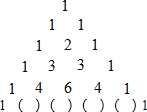
Θ®1Θ©ΆΦ÷–ΒΎΝυ––ά®Κ≈άοΒΡ ΐΉ÷Ζ÷±π «ΓΓ ΓΓΘΜΘ®«κΑ¥¥”ΉσΒΫ”“ΒΡΥ≥–ρΧν–¥Θ©
Θ®2Θ©Θ®a+bΘ©4ΘΫΓΓ ΓΓΘΜ
Θ®3Θ©άϊ”Ο…œΟφΒΡΙφ¬…ΦΤΥψ«σ÷ΒΘΚΘ®![]() Θ©4©¹4ΓΝΘ®
Θ©4©¹4ΓΝΘ®![]() Θ©3+6ΓΝΘ®
Θ©3+6ΓΝΘ®![]() Θ©2©¹4ΓΝ
Θ©2©¹4ΓΝ![]() +1Θ°
+1Θ°
Θ®4Θ©»τΘ®2x©¹1Θ©2018ΘΫa1x2018+a2x2017+a3x2016+Γ≠Γ≠+a2017x2+a2018x+a2019Θ§«σa1+a2+a3+Γ≠Γ≠+a2017+a2018ΒΡ÷ΒΘ°
ΓΨ¥πΑΗΓΩ(1) 5Θ§10Θ§10Θ§5ΘΜ(2) ![]() ΘΜ(3)
ΘΜ(3) ![]() ΘΜ(4)0
ΘΜ(4)0
ΓΨΫβΈωΓΩ
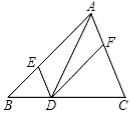
Θ®1Θ©ΗυΨίΓΑ―νΜ‘»ΐΫ«Γ±Ιφ¬…»ΖΕ®≥ωΒΎΝυ––ά®Κ≈άοΒΡ ΐΉ÷Φ¥Ω…ΘΜ
Θ®2Θ©ΗυΨίΓΑ―νΜ‘»ΐΫ«Γ±÷–ΒΡœΒ ΐ»ΖΕ®≥ω‘≠ Ϋ’ΙΩΣΫαΙϊΦ¥Ω…ΘΜ
Θ®3Θ©‘≠ ΫΡφ”ΟΓΑ―νΜ‘»ΐΫ«Γ±œΒ ΐΙφ¬…±δ–ΈΘ§ΦΤΥψΦ¥Ω…ΒΟΒΫΫαΙϊΘ°
Θ®4Θ©Β±x=0Θ§œ»«σ≥ω![]() Θ§Β±x=1 ±Θ§¥ζ»κ‘≠ ΫΦΤΥψΘ§Φ¥Ω…«σ≥ω¥πΑΗ.
Θ§Β±x=1 ±Θ§¥ζ»κ‘≠ ΫΦΤΥψΘ§Φ¥Ω…«σ≥ω¥πΑΗ.
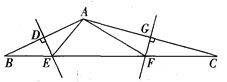
ΫβΘΚΘ®1Θ©ΗυΨίΆΦ÷–Ιφ¬…ΘΚΒΎΝυ––ά®Κ≈άοΒΡ ΐΉ÷Ζ÷±πΈΣΘΚ5Θ§10Θ§10Θ§5ΘΜ
Θ®2Θ©![]() ΘΜ
ΘΜ
Θ®3Θ©‘≠ ΫΘΫ![]() ΘΜ
ΘΜ
Θ®4Θ©Β±xΘΫ0 ±Θ§![]() Θ§
Θ§
Β±xΘΫ1 ±Θ§![]() Θ§
Θ§
Γύ![]() ΘΜ
ΘΜ

 Ϋπ≈ΤΫΧΗ®≈ύ”≈”≈―ΓΨμΤΎΡ©≥ε¥Χ100Ζ÷œΒΝ–¥πΑΗ
Ϋπ≈ΤΫΧΗ®≈ύ”≈”≈―ΓΨμΤΎΡ©≥ε¥Χ100Ζ÷œΒΝ–¥πΑΗ