题目内容
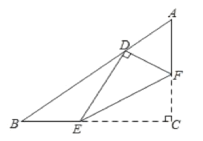
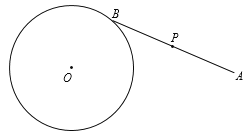
【题目】如图,⊙O的半径为2,O到定点A的距离为5,点B在⊙O上,点P是线段AB的中点.若B在⊙O上运动一周:
(1)证明点P运动的路径是一个圆.
(思路引导:要证点P运动的路径是一个圆,只要证点P到定点M的距离等于定长r,由图中的定点、定长可以发现M、r.)
(2)△ABC始终是一个等边三角形,直接写出PC长的取值范围.
【答案】(1)见解析 (2)![]() ≤PC≤
≤PC≤![]()
【解析】
(1)连接OA、OB,取OA的中点H,连接OB,HP,则HP是△ABO的中位线,HP=![]() OB=1,即可得出结论;
OB=1,即可得出结论;
(2)连接AO并延长AO交⊙O于点M、N,由等边三角形的性质得出PC⊥AB,PA=PB=![]() AB=
AB=![]() BC,得出PC=
BC,得出PC=![]() AB,分别求出PC的最小值和最大值,即可得出答案.
AB,分别求出PC的最小值和最大值,即可得出答案.
(1)证明:连接OA、OB,取OA的中点H,连接OB,HP,如图1所示:
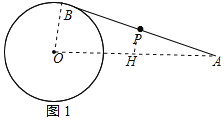
则HP是△ABO的中位线,HP=![]() OB=1,
OB=1,
∵点O与点A是定点,
∴OA的中点H也是定点,
∴B在⊙O上运动,
则点P随之运动,但HP=![]() OB=1不变,
OB=1不变,
∴B在⊙O上运动一周,点P运动的路径是以点H为圆心,半径为1的一个圆;
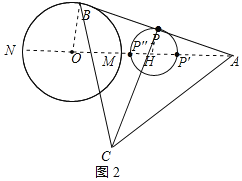
(2)解:连接AO并延长AO交⊙O于点M、N,如图2所示:
∵△ABC是等边三角形,点P是线段AB的中点,
∴PC⊥AB,PA=PB=![]() AB=
AB=![]() BC,
BC,
∴PC=![]() AB,
AB,
当点B运动到点M位置时,点P运动到点P'位置,PC最短,
∵AM=OA-OM=5-2=3,
∴AP'=![]() AM=
AM=![]() ,
,
∴PC=![]() ;
;
当点B运动到点N位置时,点P运动到点P'位置,PC最长,
∵AN=OA+ON=5+2=7,
∴AP'=![]() ,
,
∴PC=![]() ;
;
∴PC长的取值范围是![]() ≤PC≤
≤PC≤![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目