��Ŀ����
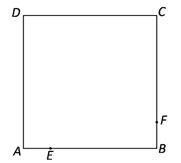
����Ŀ����ͼ����֪������ABCD�ı߳�Ϊ4 cm����E�ӵ�A��������1cm/s���ٶ���������A��B��C�˶��������Cʱֹͣ�˶�����F�ӵ�B������Ҳ��1cm/s���ٶ���������B��C��D�˶��������Dʱֹͣ�˶�����E��F�ֱ�ӵ�A��Bͬʱ���������˶�ʱ��Ϊt��s����
��1����tΪ��ֵʱ��E��F�����ľ���Ϊ2![]() cm��
cm��
��2������DE��AF���ڵ�M��
���������˶������У�CM����СֵΪ cm��
�ڵ�CM��4 cmʱ����ʱt��ֵΪ .
���𰸡���1��t1��2+![]() ��t2��2��
��t2��2��![]() �� t3��6+
�� t3��6+![]() ��t4��6��
��t4��6��![]() . ��2���� 2
. ��2���� 2![]() ��2���� 2��8.
��2���� 2��8.
��������
��1�����������ȷ��E,F��λ�ã����ݹ��ɶ�����ֵ��
��2���ٸ��������������M���˶��켣��Բ��Ȼ���������֮���߶����ȷ����Сֵ��
����֤��DAM�ա�CDN����DAE�ס�DMA��������������.
��1�� �⣺��E��F����ֱ���AB��BC��ʱ��
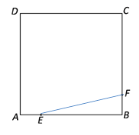
��AE= t��EB=4��t��BF= t
��EB2��BF2��EF2
��t2����4��t��2��(2![]() )2
)2
�� t1��2+![]() ��t2��2��
��t2��2��![]() .
.
��E��F����ֱ���BC��CD��ʱ��
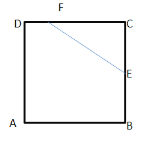
��CE=8��t��EB=t��4
��CE2��CF2��EF2
��(8��t)2����t��4��2��(2![]() )2
)2
�� t1��6+![]() ��t2��6��
��t2��6��![]() .
.
��2��
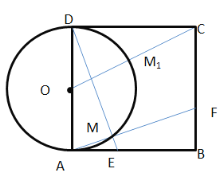
��E,F�����ٶ���ͬ����AE=BF
�֡�������ABCD�У�AD=BA,��DAB=��B=90�㣬
���DAE�ա�ABF��
���ADE=��BAF
���ADE+DAF=90�㣬����AMD=90��
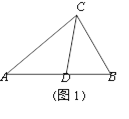
���Ե�M����OΪԲ�ģ�ADΪֱ����Բ�ϣ�����OC��ԲO�ڵ�M1,��ʱCM������̣���Rt��DOC�У�CO=![]()
����CM����СֵΪ![]() cm��
cm��
��
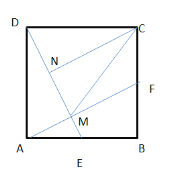
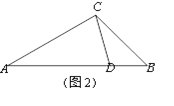
��ͼ������C��CN��DE����������֤����DAM�ա�CDN����DN=AM���֡�CM=CD=4,��CN��DE����DM=2AM,��![]()
����һ�ʿ�֪����AMD=90�㣬���DAE=��AMD,��ADM=��EDA
���DAE�ס�DMA
��![]()
��t=AE=2��
����E�����C,��F�����D����ʱAM=4����ʱt=8,
���ϣ���CM��4 cmʱ����ʱt��ֵΪ2��8.

 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д�