题目内容
【题目】已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x | … | ﹣1 | 0 | 2 | 3 | 4 | … |
y | … | 5 | 2 | 2 | 5 | 10 | … |
(1)根据上表填空: ①这个抛物线的对称轴是 , 抛物线一定会经过点(﹣2,);
②抛物线在对称轴右侧部分是(填“上升”或“下降”);
(2)如果将这个抛物线y=ax2+bx+c向上平移使它经过点(0,5),求平移后的抛物线表达式.
【答案】
(1)x=1;10;上升
(2)解:将点(﹣1,5)、(0,2)、(2,2)代入y=ax2+bx+c中,
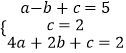 ,解得:
,解得: 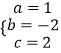 ,
,
∴二次函数的表达式为y=x2﹣2x+2.
∵点(0,5)在点(0,2)上方3个单位长度处,
∴平移后的抛物线表达式为y=x2﹣2x+5
【解析】解:(1)①∵当x=0和x=2时,y值均为2, ∴抛物线的对称轴为x=1,
∴当x=﹣2和x=4时,y值相同,
∴抛物线会经过点(﹣2,10).
所以答案是:x=1;10.
②∵抛物线的对称轴为x=1,且x=2、3、4时的y的值逐渐增大,
∴抛物线在对称轴右侧部分是上升.
所以答案是:上升.
1)①根据抛物线过点(0,2)、(2,2),即可得出抛物线的对称轴为x=1,再根据二次函数的对称性结合当x=4时y=10,即可得出当x=﹣2时y的值;②根据抛物线的对称轴为x=1结合当x=2、3、4时的y的值逐渐增大,即可得出抛物线在对称轴右侧部分是上升;(2)根据点的坐标利用待定系数法即可求出原二次函数表达式,再根据点(0,5)在点(0,2)上方3个单位长度处即可得出抛物线往上平移3个单位长度,在原二次函数表达式常数项上+3即可得出结论.
【考点精析】本题主要考查了二次函数图象的平移的相关知识点,需要掌握平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减才能正确解答此题.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案【题目】某市为美化城市,有关部门决定利用现有的4200盆甲种花卉和3090盆乙种花卉,搭配成A、B两种园艺造型共60个,摆放于主干街道的两侧,搭配每个造型所需花卉数量的情况如下表所示,结合上述信息,解答下列问题:
造型花卉 | 甲 | 乙 |
A | 80 | 40 |
B | 50 | 70 |
(1)符合题意的搭配方案有几种?
(2)如果搭配一个A种造型的成本为600元,搭配一个B种造型的成本为800元,试说明选用那种方案成本最低?最低成本为多少元?