题目内容
【题目】已知:如图,在△ABC中,点D,E分别在边AB,BC上,BABD=BCBE 
(1)求证:DEAB=ACBE;
(2)如果AC2=ADAB,求证:AE=AC.
【答案】
(1)证明:∵BABD=BCBE,
∴ ![]() ,
,
又∵∠B=∠B,
∴△ABC∽△EBD,
∴ ![]() ,
,
∴DEAB=ACBE;
(2)证明:∵AC2=ADAB,
∴ ![]() ,
,
∵∠DAC=∠CAB,
∴△ADC∽△ACB,
∴∠ACD=∠B,
∵ ![]() ,∠B=∠B,
,∠B=∠B,
∴△BAE∽△BCD,
∴∠BAE=∠BCD,
∵∠AEC=∠B+∠BAE,∠ACE=∠ACD+∠BCD,
∴∠AEC=∠ACE,
∴AE=AC.
【解析】(1)由BABD=BCBE得 ![]() ,结合∠B=∠B,证△ABC∽△EBD得
,结合∠B=∠B,证△ABC∽△EBD得 ![]() ,即可得证;(2)先根据AC2=ADAB证△ADC∽△ACB得∠ACD=∠B,再由
,即可得证;(2)先根据AC2=ADAB证△ADC∽△ACB得∠ACD=∠B,再由 ![]() 证△BAE∽△BCD得∠BAE=∠BCD,根据∠AEC=∠B+∠BAE,∠ACE=∠ACD+∠BCD可得∠AEC=∠ACE,即可得证.
证△BAE∽△BCD得∠BAE=∠BCD,根据∠AEC=∠B+∠BAE,∠ACE=∠ACD+∠BCD可得∠AEC=∠ACE,即可得证.
【考点精析】通过灵活运用相似三角形的判定与性质,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
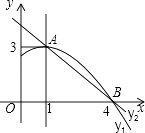
小学生10分钟应用题系列答案【题目】已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x | … | ﹣1 | 0 | 2 | 3 | 4 | … |
y | … | 5 | 2 | 2 | 5 | 10 | … |
(1)根据上表填空: ①这个抛物线的对称轴是 , 抛物线一定会经过点(﹣2,);
②抛物线在对称轴右侧部分是(填“上升”或“下降”);
(2)如果将这个抛物线y=ax2+bx+c向上平移使它经过点(0,5),求平移后的抛物线表达式.
【题目】秋季新学期开学时,红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试,测试成绩全部合格,现学校随机选取了部分学生的成绩,整理并制作成了如下不完整的图表:
分 数 段 | 频数 | 频率 |
60≤x<70 | 9 | a |
70≤x<80 | 36 | 0.4 |
80≤x<90 | 27 | b |
90≤x≤100 | c | 0.2 |

请根据上述统计图表,解答下列问题:
(1)在表中,a= , b= , c=;
(2)补全频数直方图;
(3)根据以上选取的数据,计算七年级学生的平均成绩.
(4)如果测试成绩不低于80分者为“优秀”等次,请你估计全校七年级的800名学生中,“优秀”等次的学生约有多少人?