题目内容
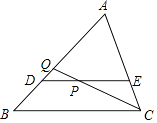
【题目】已知,如图,Rt△ABC中,∠ACB=90°,BC=8,cot∠BAC= ![]() ,点D在边BC上(不与点B、C重合),点E在边BC的延长线上,∠DAE=∠BAC,点F在线段AE上,∠ACF=∠B.设BD=x.
,点D在边BC上(不与点B、C重合),点E在边BC的延长线上,∠DAE=∠BAC,点F在线段AE上,∠ACF=∠B.设BD=x.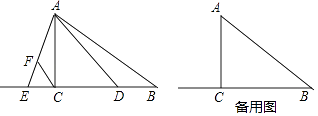
(1)若点F恰好是AE的中点,求线段BD的长;
(2)若y= ![]() ,求y关于x的函数关系式,并写出它的定义域;
,求y关于x的函数关系式,并写出它的定义域;
(3)当△ADE是以AD为腰的等腰三角形时,求线段BD的长.
【答案】
(1)
解:在Rt△ABC中,∠ACB=90°,BC=8,cot∠BAC= ![]() ,
,
∴AC=6,AB=10,
∵∠DAE=∠BAC,
∴∠FAC=∠DAB,
∵∠ACF=∠B,
∴△ABD∽△ACF,
∴ ![]() ,
,
在Rt△ABC中,点F恰好是AE的中点,
∴CF= ![]() AE=AF,
AE=AF,
∴AD=BD,
在Rt△ACD中,AC=6,CD=BC﹣BD=BC﹣AD=8﹣AD,
根据勾股定理得,AC2+CD2=AD2,
∴36+(8﹣AD)2=AD2,
∴AD= ![]() ,
,
∴BD=AD= ![]()
(2)
解:如图1,过点F作FM⊥AC于M,
由(1)知,∴ ![]() =
= ![]() ,
,
∴CF= ![]() =
= ![]() ×x=
×x= ![]() x,
x,
由(1)△ABD∽△ACF,
∴∠B=∠ACF,
∴tan∠ACF=tanB= ![]() =
= ![]() =
= ![]() ,
,
∴MC= ![]() x,
x,
∴y= ![]() =
= ![]() =
= ![]() (0<x<8)
(0<x<8)
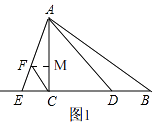
(3)
解:∵△ADE是以AD为腰的等腰三角形,
∴①当AD=AE时,
∴∠AED=∠ADE,
∵∠ACD=90°,
∴∠EAC=∠DAC=∠DAB,
∴AD是∠BAC的平分线,
∴ ![]() ,
,
∵AC=6,AB=10,CD=8﹣BD,
∴ ![]() ,
,
∴BD=5,
当AD=DE时,
∴∠DAE=∠DEA=∠BAC,
∴∠ADE=2∠B,
∴∠B=∠DAB,
∴AD=BD= ![]() (是(1)的那种情况).
(是(1)的那种情况).
即:BD=5或BD= ![]() 时,△ADE是以AD为腰的等腰三角形.
时,△ADE是以AD为腰的等腰三角形.
【解析】(1)先判断出△ABD∽△ACF,进而判断出AD=BD,再用解直角三角形的方法即可得出BD;(2)先表示出CF,进而表示出MC,即可得出函数关系式;(3)分两种情况列出方程求解即可得出结论.
【考点精析】利用三角形的外角和全等三角形的性质对题目进行判断即可得到答案,需要熟知三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;全等三角形的对应边相等; 全等三角形的对应角相等.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x | … | ﹣1 | 0 | 2 | 3 | 4 | … |
y | … | 5 | 2 | 2 | 5 | 10 | … |
(1)根据上表填空: ①这个抛物线的对称轴是 , 抛物线一定会经过点(﹣2,);
②抛物线在对称轴右侧部分是(填“上升”或“下降”);
(2)如果将这个抛物线y=ax2+bx+c向上平移使它经过点(0,5),求平移后的抛物线表达式.