题目内容
【题目】某校兴趣小组想测量一座大楼AB的高度.如图6,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1: ![]() .在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米) (参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
.在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米) (参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, ![]() ≈1.73.)
≈1.73.)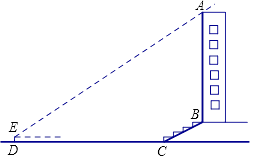
【答案】解:延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H. ∵在Rt△BCF中, ![]() =i=1:
=i=1: ![]() ,
,
∴设BF=k,则CF= ![]() ,BC=2k.
,BC=2k.
又∵BC=12,
∴k=6,
∴BF=6,CF= ![]() .
.
∵DF=DC+CF,
∴DF=40+6 ![]() .
.
∵在Rt△AEH中,tan∠AEH= ![]() ,
,
∴AH=tan37°×(40+6 ![]() )≈37.8(米),
)≈37.8(米),
∵BH=BF﹣FH,
∴BH=6﹣1.5=4.5.
∵AB=AH﹣HB,
∴AB=37.8﹣4.5=33.3.
答:大楼AB的高度约为33.3米.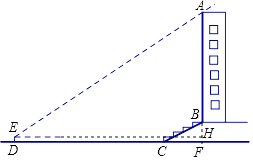
【解析】延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H,在Rt△BCF中利用坡度的定义求得CF的长,则DF即可求得,然后在直角△AEH中利用三角函数求得AF的长,进而求得AB的长.

练习册系列答案
相关题目
【题目】已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x | … | ﹣1 | 0 | 2 | 3 | 4 | … |
y | … | 5 | 2 | 2 | 5 | 10 | … |
(1)根据上表填空: ①这个抛物线的对称轴是 , 抛物线一定会经过点(﹣2,);
②抛物线在对称轴右侧部分是(填“上升”或“下降”);
(2)如果将这个抛物线y=ax2+bx+c向上平移使它经过点(0,5),求平移后的抛物线表达式.