题目内容
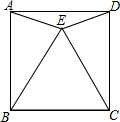
如图,在正方形ABCD,F为DC的中点,E为BC上一点,且EC=
BC.
(1)求证:AF⊥EF;
(2)若△AEF的面积为5,求正方形ABCD的边长.

| 1 |
| 4 |
(1)求证:AF⊥EF;
(2)若△AEF的面积为5,求正方形ABCD的边长.

证明:(1):∵四边形ABCD是正方形,
∴∠C=∠D=90°,
∵F是CD中点,
∴DF=CF=
CD=
AD,
∵CE=
BC=
CD,
∴CE:DF=CF:AD=1:2,
∴Rt△CEF∽Rt△DFA,
∴∠FAD=∠EFC,
∵∠DAF+∠DFA=90°,
∴∠EFC+∠DFA=90°,
∴∠EFA=180°-90°=90°.
∴AF⊥EF;
(2)设CE=x,则DF=CF=2x,AD=4x,
S△AEF=
×2
x×
x=5,
解之得,x=1
所以正方形的边长为4x=4.
∴∠C=∠D=90°,
∵F是CD中点,
∴DF=CF=
| 1 |
| 2 |
| 1 |
| 2 |
∵CE=
| 1 |
| 4 |
| 1 |
| 4 |
∴CE:DF=CF:AD=1:2,
∴Rt△CEF∽Rt△DFA,
∴∠FAD=∠EFC,
∵∠DAF+∠DFA=90°,
∴∠EFC+∠DFA=90°,
∴∠EFA=180°-90°=90°.
∴AF⊥EF;
(2)设CE=x,则DF=CF=2x,AD=4x,
S△AEF=
| 1 |
| 2 |
| 5 |
| 5 |
解之得,x=1
所以正方形的边长为4x=4.

练习册系列答案
相关题目