题目内容
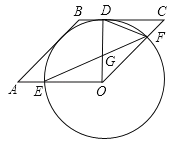
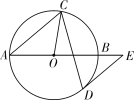
【题目】如图，AB是⊙O的直径，弦CD与AB相交，连接CO，过点D作⊙O的切线，与AB的延长线交于点E，若DE∥AC，∠BAC＝40°，则∠OCD的度数为（ ）
A.65°B.30°C.25°D.20°
【答案】C
【解析】
连接OD，如图，先利用平行线的性质得∠E=∠BAC=40°，再根据切线的性质得OD⊥DE，则可计算出∠DOE=50°，接着根据圆周角定理得到∠BOC=2∠A=80°．然后根据等腰三角形的性质和三角形内角和计算∠OCD的度数．
连接OD，如图，
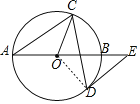
∵DE∥AC，
∴∠E=∠BAC=40°，
∵DE为切线，
∴OD⊥DE，
∴∠DOE=90°-40°=50°，
∵∠BOC=2∠A=80°．
∴∠COD=80°+50°=130°，
∵OC=OD，
∴∠OCD=∠ODC=
（180°-130°）=25°．
故选：C．
练习册系列答案
相关题目
