Question

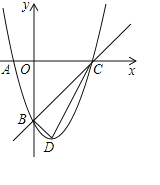
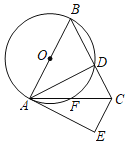
【题目】如图，在平面直角坐标系中，点是轴正半轴上的一动点，抛物线(是常数，且过点，与轴交于两点，点在点左侧，连接，以为边做等边三角形，点与点在直线两侧．

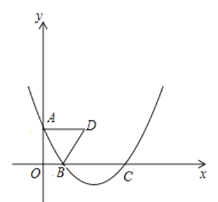
（1）求B、C的坐标；

（2）当轴时，求抛物线的函数表达式；

（3）①求动点所成的图像的函数表达式；

②连接，求的最小值．

Answer 1

【答案】（1）、；（2）；（3）①；②．

【解析】

（1），令，则或4，即可求解；

（2）当轴时，则，则，故点，即可求解；

（3）构造一线三垂直相似模型由，则，解得：，，故点，，即可求解．

解：（1）当时，即，

解得或4，

故点、的坐标分别为：、；

（2）∵等边三角形，

∴，

∴当轴时，，

∴，故点，

即，解得：，

故抛物线的表达式为：；

（3）①如图，过点作于点，过点作轴的垂线于点，过点作轴交轴于点交于点，

为等边三角形，

∴点为的中点， ，

∴点，，

，，

，

，

，其中，，

解得：，，故点，，

即动点所成的图像的函数满足 ，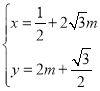

∴动点所成的图像的函数表达式为：．

②由①得点，，

∴，

故当时，的最小值为，即的最小值为．