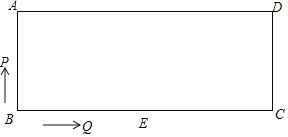题目内容
【题目】如图,点M是矩形ABCD的边AD的中点,点P是BC边上一动点,PE⊥MC,PF⊥BM,垂足为E、F.
(1)当矩形ABCD的长与宽满足什么条件时,四边形PEMF为矩形?猜想并证明你的结论.
(2)在(1)中,当点P运动到什么位置时,矩形PEMF变为正方形,为什么?
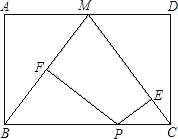
【答案】(1) 当AD=2AB时,四边形PEMF为矩形,理由见解析;(2) 当P是BC的中点时,矩形PEMF为正方形,理由见解析
【解析】
(1)根据矩形的性质推出∠A=∠D=90°,AB=CD,AM=DM,求出∠ABM=∠AMB=45°,∠DCM=∠DMC=45°,求出∠BMC,即可求出矩形PEMF.
(2)根据AAS证△BFP≌△CEP,推出PE=PF即可.
(1)当AD=2AB时,四边形PEMF为矩形.
证明:∵四边形ABCD为矩形,
∴∠A=∠D=90°,
∵AD=2AB=2CD,AM=DM=![]() AD,
AD,
∴AB=AM=DM=CD,
∴∠ABM=∠AMB=45°,∠DCM=∠DMC=45°,
∴∠BMC=180°-45°-45°=90°,
∵PE⊥MC,PF⊥BM,
∴∠MEP=∠FPE=90°,
∴四边形PEMF为矩形,
即当AD=2AB时,四边形PEMF为矩形;
(2)当P是BC的中点时,矩形PEMF为正方形.
理由是:∵四边形PEMF为矩形,
∴∠PFM=∠PFB=∠PEC=90°,
在△BFP和△CEP中
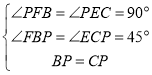 ,
,
∴△BFP≌△CEP(AAS),
∴PE=PF,
∵四边形PEMF是矩形,
∴矩形PEMF是正方形,
即当P是BC的中点时,矩形PEMF为正方形.

练习册系列答案
相关题目