题目内容
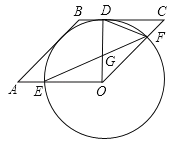
【题目】已知:四边形OABC是菱形,以O为圆心作⊙O,与BC相切于点D,交OA于E,交OC于F,连接OD,DF.
(1)求证:AB是⊙O的切线;
(2)连接EF交OD于点G,若∠C=45°,求证:GF2=DGOE.
【答案】(1)证明见解析;(2)证明见解析.
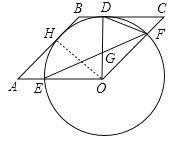
【解析】试题分析:(1)过O作OH⊥AB,由菱形的性质可求得OH=OD,由切线的性质可知OD为圆O的半径,可得OH为圆O的半径,可证得结论;
(2)由条件可证明△DGF∽△DFO,再利用相似三角形的性质可证得结论.
试题解析:解:
(1)如图,过O作OH⊥AB,∵四边形OABC为菱形,∴AB=BC,∵BC为⊙O的切线,∴OD⊥BC,且OD为⊙O的半径,∴ABOH=BCOD,∴OH=OD,∴AB为⊙O的切线;
(2)由(1)可知OD⊥CB,∴AO⊥DO,∴∠AOD=90°,∴∠DFO=![]() ∠AOD=45°,∵∠C=45°,且∠ODC=90°,∴∠DOF=45°,在△OGF中,∠DGF为△OGF的外角,∴∠DGF=∠DOF+∠GFO=45°+∠GFO,∵∠DFO=∠DFG+∠GFO=45°+∠GFO,∴∠DGF=∠DFO,且∠GDF=∠FDO,∴△DGF∽△DFO,∴
∠AOD=45°,∵∠C=45°,且∠ODC=90°,∴∠DOF=45°,在△OGF中,∠DGF为△OGF的外角,∴∠DGF=∠DOF+∠GFO=45°+∠GFO,∵∠DFO=∠DFG+∠GFO=45°+∠GFO,∴∠DGF=∠DFO,且∠GDF=∠FDO,∴△DGF∽△DFO,∴![]() ,即DFGF=DGOF,∵OF=OD=OE,∴DF=GF,∴GF2=DGOE.
,即DFGF=DGOF,∵OF=OD=OE,∴DF=GF,∴GF2=DGOE.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
【题目】某校为了了解七年级学生的学习情况,在这个年级抽取了50名学生对某课进行了测试。将所得的成绩(成绩均为整数)进行整理(如下边所示),请你画出频数分布直方图和频数折线图,并回答问题:
分数 |
|
|
|
|
|
频率 | 0.04 | 0.04 | 0.16 | 0.34 | 0.42 |
![]() 这次测试及格(包括60分)的人数有多少?
这次测试及格(包括60分)的人数有多少?
![]() 本次测试这50名学生成绩的优秀率是多少?(90分以上为优秀,包括90分)
本次测试这50名学生成绩的优秀率是多少?(90分以上为优秀,包括90分)
![]() 这个年级此学科学习情况如何?
这个年级此学科学习情况如何?
