题目内容
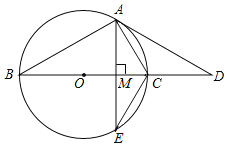
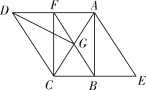
【题目】如图,在ABC中,∠ABC=90°,∠ACB=60°,将ABC绕点C逆时针旋转60°得到DGC,再将ABC沿AB所在直线翻折得到ABE,连接AD,BG,延长BG交AD于点F,连接CF.
(1)求证:四边形ABCF是矩形;
(2)若GF=2![]() ,求四边形AECD的面积.
,求四边形AECD的面积.
【答案】(1)见解析;(2)24![]()
【解析】
(1)由旋转的性质可得AC=CD,∠DCG=∠ACB=60°,CG=CB,可证△ACD是等边三角形,△CBG是等边三角形,可得∠DAC=∠CGB=∠AGF=60°,BG=BC=CG,由直角三角形的性质可得AG=CG=BC,由矩形的判定可得结论;
(2)先证四边形AECD是菱形,由菱形的面积公式可求解.
(1)∵△ABC绕点C旋转得到△DGC,
∴AC=CD,∠DCG=∠ACB=60°,
∴△ACD是等边三角形,
∴∠DAC=60°
∵在Rt△DGC中,∠CDG=30°,
∴DC=2CG=AC,
∴AG=GC=BC,
∴∠CGB=∠AGF=60°,
∴△CBG和△AGF都是等边三角形,
∴AG=GC=BG=GF,
∴四边形ABCF是矩形;
(2)∵△ABC绕点C旋转得到△DGC,△ABC沿AB所在直线翻折得到△ABE,∠ABC=90°,∠ACB=60°,
∴DC=AC=AE,∠DCG=∠ACB=∠AEC=60°,
∴∠AEC+∠DCE=180°,
∴DC∥AE,
∴四边形AECD为平行四边形.
又∵AC=2CB,
∴AC=CE=AE,
∴四边形AECD为菱形
∵GF=2![]() ,
,
∴AC=CE=4![]() ,CB=2
,CB=2![]() ,
,
∴AB=![]() =6,
=6,
∴S四边形AECD=4![]() ×6=24
×6=24![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目