��Ŀ����
����Ŀ���Ķ�������ϣ���ɣ�1��-��3����
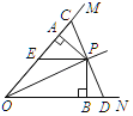
��ѧ���ϣ���ʦ��ʾ������һ���⣺��ͼ����ABD�͡�ACE�У�AB��AD��AC��AE����DAB����CAE����������DC��BE���ڵ�F����A��AG��DC�ڵ�G��̽���߶�FG��FE��FC֮���������ϵ����֤����
ͬѧ�Ǿ���˼�����������ѵ��뷨��
С������ͨ���۲�Ͷ����������߶�BE���߶�DC��ȣ���
Сΰ����ͨ���۲췢�֣���AFE��������ij��������ϵ����
��ʦ����ͨ������ȫ�������Σ��Ӷ�����̽�����߶�FG��FE��FC֮���������ϵ����
��1����֤��BE��CD��
��2�����AFE�Ķ������ú�����ʽ�ӱ�ʾ����
��3��̽���߶�FG��FE��FC֮���������ϵ����֤����
���𰸡���1������������2����AFE��![]() ����3��EF��FC+2GF��������
����3��EF��FC+2GF��������
��������
��1���ɡ�DAB����CAE�������ɵá�DAC����BAE��������SAS����֤��ADC�ա�ABE���ɵ�DC��BE��
��2������ADC�ա�ABE�ɵá�AEF����ACD������֤��A����E����C����F�ĵ㹲Բ���ɵá�AFE����ACE�����ݵ��������ε����ʺ��������ڽǺͶ��������AFE�Ķ�����
��3�����ۣ�EF��FC+2GF��������ɵá�AFD��![]() ����AFE��������AH��BE����֤��AGF�ա�AHF���ɵ�AG��AH��GF��HF������֤Rt��AGC��Rt��AHE���ɵ�GC��HE����EF��FC��2GF�ɵý��ۣ�
����AFE��������AH��BE����֤��AGF�ա�AHF���ɵ�AG��AH��GF��HF������֤Rt��AGC��Rt��AHE���ɵ�GC��HE����EF��FC��2GF�ɵý��ۣ�
֤������1���ߡ�DAB����CAE������
���DAC����BAE����AD��AB��AC��AE
���ADC�ա�ABE��SAS��
��DC��BE��
��2���ߡ�ADC�ա�ABE
���AEF����ACD
���A����E����C����F�ĵ㹲Բ
���AFE����ACE
��AC��AE����DAB����CAE����
���ACE��![]() ��
��
���AFE��![]() ��
��
��3�����ۣ�EF��FC+2GF��
���ɣ��ߡ�ADC�ա�ABE
���ADC����ABE
���A����D����B����F�ĵ㹲Բ
���AFD����ABD
��AB��AD����DAB����CAE����
���ABD��![]() ��
��
���AFD��![]() ��
��
���AFE����AFD
��ͼ��������AH��BE��
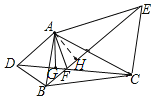
�ߡ�AFE����AFD����AGF����AHF��AF��AF
���AGF�ա�AHF��AAS��
��AG��AH��GF��HF��
��AG��AH��AE��AC
��Rt��AGC��Rt��AHE��HL��
��GC��HE
��EF��FC��HE+FH��FC��GC+FH��FC��GF+FC+FH��FC��2GF��
��EF��FC+2GF��