Question

【题目】如图，已知的直径为，的度数为，点是的中点，在直径上作出点，使的值最小，则的最小值为________．

Answer 1

【答案】

【解析】

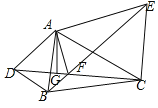
作B关于CD的对称点E，则E正好在圆周上连接OA、OB、OE、AE，AE交CD于P，则AP+BP最短，根据 的度数为60°，点B是的中点计算出，∠AOB=∠COB=30°，然后再证明△OAE是等腰直角三角形，再利用勾股定理可得答案．

作B关于CD的对称点E，则E正好在圆周上，
连接OA、OB、OE、AE，AE交CD于P，
则AP+BP最短，
∵的度数为60°，点B是的中点，
∴= ，且的度数是30°，
∴∠AOB=∠COB=30°，
∵B关于CD的对称点是E，
∴弧BE的度数是60°，
∴∠AOE=90°，
∵OA=OE=CD=1，
∴△OAE是等腰直角三角形，
由勾股定理得：AE= ．
故答案是：．