Question

【题目】如图，的半径为，弦、的长度分别为，则弦、所夹的锐角为________．

Answer 1

【答案】

【解析】

作OE⊥AB于E，OF⊥DC于F，连结OA、OB、OC、OD、BC，根据垂径定理得BE= AB=，CF=DC=，在利用正弦的定义可分别求出∠3=60°，∠4=30°，则根据等腰三角形的性质得∠AOB=2∠3=120°，∠COD=2∠4=60°，然后根据圆周角定理得∠2=60°，∠1=30°，最后利用三角形外角性质求解．

作OE⊥AB于E，OF⊥DC于F，连结OA、OB、OC、OD、BC，如图所示：

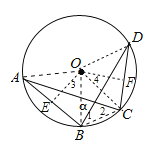
则AE=BE=AB=，CF=DF=DC=，
在Rt△BOE中，BE=，OB=1，
∴sin∠3=，
∴∠3=60°，
在Rt△OCF中，CF=，OC=1，
∴sin∠4=，
∴∠4=30°，
∵OA=OB，OC=OD，
∴∠AOB=2∠3=120°，∠COD=2∠4=60°，
∴∠2=∠AOB=60°，∠1=∠COD=30°
∴∠α=∠1+∠2=90°．
故答案是：90°．