Question

【题目】如图，已知AD、AE分别是△ABC的中线、高，且AB=4cm，AC=3cm，请解答下列问题：

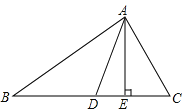
(1)△ABD与△ACD的面积大小有怎样的关系？并说明理由.

(2)△ABD与△ACD的周长之差是多少？

(3)当AE=2.5cm ，BC=6cm时，试求△ABD的面积.

Answer 1

【答案】（1）△ABD和△ACD的面积相等，理由见解析；（2）1 ；（3）S△ABD＝3.75 cm2

【解析】

（1）根据三角形面积公式即可比较判断；

（2）根据周长的定义即可比较判断；

（3）根据三角形的面积公式代入即可求解.

（1）△ABD和△ACD的面积相等，

理由如下：

∵AD、AE分别是△ABC的中线和高

∴BD=CD

S△ABD=，S△ACD=

∴S△ABD= S△ACD

（2）△ABD的周长=AB+BD+AD=4+BD+AD

△ACD的周长=AC+DC+AD=3+DC+AD

∵BD=DC

∴（4+BD+AD）-（3+DC+AD）

=1

（3）当AE=2.5 cm，BC=6 cm时，BD＝BC＝3cm

∴S△ABD＝=＝3.75 cm2