题目内容
【题目】四边形ABCD中,点E在边AB上,连结DE,CE.
(1)若∠A=∠B=∠DEC=50°,找出图中的相似三角形,并说明理由;
(2)若四边形ABCD为矩形,AB=5,BC=2,且图中的三个三角形都相似,求AE的长.
(3)若∠A=∠B=90°,AD<BC,图中的三个三角形都相似,请判断AE和BE的数量关系并说明理由.

【答案】(1)△DAE∽△EBC,理由见解析;(2)AE=1或4;(3)AE=BE或BE=2AE,理由见解析.
【解析】
(1)三角形内角和为180°,所以∠ADE+∠DEA=180°﹣∠A=130°,又因为∠DEA+∠CEB=180°﹣∠DEC=130°,所以∠ADE=∠CEB,已知∠A=∠B,所以△DAE∽△EBC;
(2)设AE=x,则BE=5﹣x,不难证明△DAE∽△EBC,根据相似三角形的性质列方程求出x即可;(3)分两类进行讨论:①∠A=∠B=∠DEC=90°,②∠DEC≠90°,结合相似三角形的性质分别求出AE和BE的数量关系.
(1)△DAE∽△EBC,
理由:∵∠A=∠DEC=50°,
∴∠ADE+∠DEA=180°﹣∠A=130°,∠DEA+∠CEB=180°﹣∠DEC=130°,
∴∠ADE=∠CEB,
∵∠A=∠B,
∴△DAE∽△EBC;
(2)
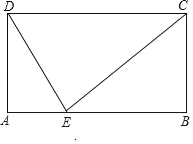
设AE=x,则BE=5﹣x,
∵矩形ABCD,
∴∠A=∠B=∠ADC=∠BCD=90°,
∵图中三个三角形都相似,
∴△DEC为直角三角形,
∵∠EDC<90°,∠ECD<90°,
∴∠DEC=90°,
∴∠ADE+∠AED=90°,
∵AED+∠CEB=90°,
∴∠AED=∠ECB,
∴△DAE∽△EBC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:x=1或4,
即AE=1或4;
(3)AE=BE或BE=2AE,
理由:①
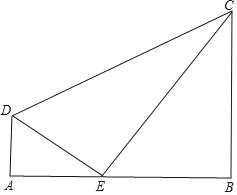
当∠A=∠B=∠DEC=90°时,∠DCE≠∠CEB,可得∠DCE=∠BCE,
所以△DEC∽△DAE∽△EBC,
∴![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,即BE=AE;
,即BE=AE;
②当∠DEC≠90°时,
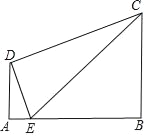
如图,∵AD<BC,
∴∠CDE=90°,
∵∠DCE≠∠CEB,
∴∠DCE=∠ECB,∠DEC=∠CEB,
∴DE=BE,
∵∠ADE≠∠DEC,
∴∠ADE=∠DCE,∠AED=∠DEC,
∴∠AED=∠DEC=∠CEB=60°,
∴![]() =
=![]() =cos60°=
=cos60°=![]() ,
,
∴BE=2AE.

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案