题目内容
【题目】如图22,在∠AOB的两边OA,OB上分别取OM=ON,OD=OE,DN和EM相交于点C.求证:点C在∠AOB的平分线上.
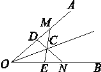
【答案】见解析
【解析】
过点C分别作CG⊥OA于点G,CF⊥OB于点F,在△MOE和△NOD中,根据OM=ON,∠MOE=∠NOD,OE=OD,可判定△MOE≌△NOD,根据全等三角形的性质可得:S△MOE=S△NOD,继而可得S△MOE-S四边形ODCE=S△NOD-S四边形ODCE,即S△MDC=S△NEC.
由三角形面积公式得DM·CG=EN·CF.由于OM=ON,OD=OE,所以DM=EN,CG=CF.
根据CG⊥OA,CF⊥OB,可证点C在∠AOB的平分线上.
证明:过点C分别作CG⊥OA于点G,CF⊥OB于点F,
如图.

在△MOE和△NOD中,OM=ON,∠MOE=∠NOD,OE=OD,
∴△MOE≌△NOD(SAS),
∴S△MOE=S△NOD,
∴S△MOE-S四边形ODCE=S△NOD-S四边形ODCE,
即S△MDC=S△NEC.
由三角形面积公式得DM·CG=EN·CF.
∵OM=ON,OD=OE,
∴DM=EN,
∴CG=CF.
又∵CG⊥OA,CF⊥OB,
∴点C在∠AOB的平分线上.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目