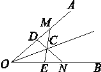题目内容
【题目】如图,正方形ABCD和正方形CGEF的边长分别是3和5,且点B、C、G在同一直线上,M是线段AE的中点,连接MF,则MF的长为 . 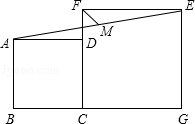
【答案】![]()
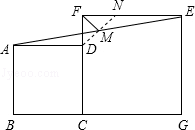
【解析】解:连接DM并延长交EF于N,如图, ∵四边形ABCD,四边形EFCG都是正方形,
∴AD∥BG,EF∥BG,
∴EF∥AD,
∴∠NEM=∠DAM,
在△ADM和△ENM中,
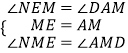
∴△ADM≌△ENM,
∴AD=NE=3,DM=MN,
∵EF=5,
∴FN=2,
∵DF=FC﹣CD=2,
∴FN=FD,
∴FM是等腰直角△DFN的底边上的中线,所以FM= ![]() DN=
DN= ![]() .
.
所以答案是: ![]() .
.
【考点精析】掌握勾股定理的概念和三角形中位线定理是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.

练习册系列答案
相关题目