题目内容
【题目】如图,在热气球上A处测得塔顶B的仰角为52°,测得塔底C的俯角为45°,已知A处距地面98米,求塔高BC.(结果精确到0.1米)
【参考数据:sin52°=0.79,cos52°=0.62,tan52°=1.28】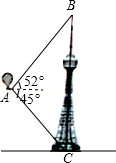
【答案】解:如图,过点A作AD⊥BC于点D.
由题意可知,在Rt△ADC中,
∠ADC=90°,∠CAD=45°,CD=98,
∴∠ACD=∠CAD=45°.
∴AD=CD=98.
在Rt△ABD中,
BD=AD×tan∠BAD=98×1.28=125.44.
∴BC=BD+CD=125.44+98=223.44≈223.4(米).
答:塔高BC约为223.4米.
【解析】过点A作AD⊥BC于点D,根据∠ACD=∠CAD=45°求出∠ACD=∠CAD=45°,从而得到AD=CD=98,再在Rt△ABD中,求出BC的长.
【考点精析】通过灵活运用关于仰角俯角问题,掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角即可以解答此题.

练习册系列答案
相关题目
【题目】为了进一步普及足球知识,传播足球文化,我市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
请根据所给信息,解答下列问题:
(1)a= , b= , 且补全频数分布直方图;
(2)若用扇形统计图来描述获奖分布情况,问获得优胜奖对应的扇形圆心角的度数是多少?
(3)若我市初中生共有16000人,竞赛活动获奖率为40%,获三等奖以上的学生表示对“足球比较喜欢”,请你估计我市初中生对“足球比较喜欢”的有多少人?