��Ŀ����
����Ŀ��̽����
�������֣�
���ν���ǽ����ѧ�����һ����Ҫ��˼�뷽�����������ַ����ɽ��������ѧ֪ʶ���ֱ���������Ҿ��пɲ����ԣ��Ӷ����������ǿ��ٽ��⣮������ѧ���һЩ������ʽ���ܶ����ͨ����ʾ����ͼ������ķ�������ֱ���Ƶ��ͽ��ͣ�
���磺����ͼ�εļ�������֤����ȫƽ����ʽ��
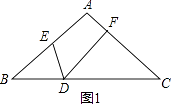
֤������һ���߳�Ϊa�������εı߳�����b���γ��������κ����������Σ���ͼ1��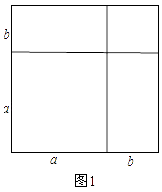
���ͼ�ε�������Ա�ʾ�ɣ�
��a+b��2��a2+2ab+b2
�ࣨa+b��2 =a2+2ab+b2
�����֤�������͵���ȫƽ����ʽ��
��1����Ƚ����
���������������������ͼ�εļ�������֤��ƽ���ʽ����Ҫ��ͼ�β�д���������̣�
��2������������������ͼ�μ�������ķ���֤����13+23=32��
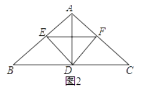
��ͼ2��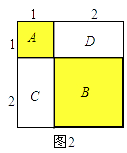
A��ʾ1��1��1�������Σ�����1��1��1=13
B��ʾ1��2��2�������Σ�C��Dǡ�ÿ���ƴ��1��2��2�������Σ���ˣ�B��C��D�Ϳ��Ա�ʾ2��2��2�������Σ�����2��2��2=23
��A��B��C��Dǡ�ÿ���ƴ��һ����1+2������1+2���Ĵ������Σ�
�ɴ˿ɵã�13+23=��1+2��2=32
���Խ����
������������Ƶ����̣�����ͼ�εļ�������ȷ����13+23+33= �� ��Ҫ��д�����۲�����ͼ��д����֤���̣���
��3�������ع㣺
��������ı�ʾ����ͼ������ķ���̽����13+23+33+��+n3= �� ��ֱ��д�����ۼ��ɣ�����д��������̣�
���𰸡�
��1��
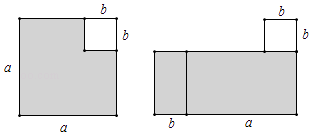
�⣺����ͼ����ͼ����Ӱ���ֵ������a2��b2��
��ͼ����Ӱ���ֵ�����ǣ�a+b����a��b����
��a2��b2=��a+b����a��b����
�����֤��ƽ���ʽ��
��2����ͼ��A��ʾ1��1��1�������Σ���1��1��1=13��
B��ʾ1��2��2�������Σ�C��Dǡ�ÿ���ƴ��1��2��2�������Σ�
��ˣ�B��C��D�Ϳ��Ա�ʾ2��2��2�������Σ�����2��2��2=23��
G��H��E��F���Ա�ʾ3��3��3�������Σ���3��3��3=33��
������ͼ��ǡ�ÿ���ƴ��һ����1+2+3������1+2+3���Ĵ������Σ�
�ɴ˿ɵã�13+23+33=��1+2+3��2=62��
�ʴ�Ϊ��62�� 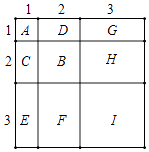
��3���⣺[ ![]() n��n+1��]2
n��n+1��]2
����������3���������ʾ����ͼ�ε����̽����֪��13+23+33+��+n3=��1+2+3+��+n��2 ��
�֡�1+2+3+��+n= ![]() n��n+1����
n��n+1����
��13+23+33+��+n3=[ ![]() n��n+1��]2 ��
n��n+1��]2 ��
���Դ��ǣ�[ ![]() n��n+1��]2 ��
n��n+1��]2 ��

 ������ÿ�ʱ�Ż���ҵϵ�д�
������ÿ�ʱ�Ż���ҵϵ�д�