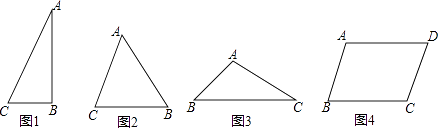题目内容
【题目】△ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,∠EDF=∠B.
(1)如图1,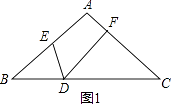
求证:DECD=DFBE
(2)D为BC中点如图2,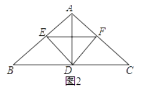
连接EF.
①求证:ED平分∠BEF;
②若四边形AEDF为菱形,求∠BAC的度数及 ![]() 的值.
的值.
【答案】
(1)
证明:∵△ABC中,AB=AC,
∴∠B=∠C.
∵∠B+∠BDE+∠DEB=180°,∠BDE+∠EDF+∠FDC=180°,∠EDF=∠B,
∴∠FDC=∠DEB,
∴△BDE∽△CFD,
∴ ![]() ,
,
即DECD=DFBE
(2)
解:①由(1)证得△BDE∽△CFD,
∴ ![]() ,
,
∵D为BC中点,
∴BD=CD,
∴ ![]() =
= ![]() ,
,
∵∠B=∠EDF,
∴△BDE∽△DEF,
∴∠BED=∠DEF,
∴ED平分∠BEF;②∵四边形AEDF为菱形,
∴∠AEF=∠DEF,
∵∠BED=∠DEF,
∴∠AEF=60°,
∵AE=AF,
∴∠BAC=60°,
∵∠BAC=60°,
∴△ABC是等边三角形,
∴∠B=60°,
∴△BED是等边三角形,
∴BE=DE,
∵AE=DE,
∴AE= ![]() AB,
AB,
∴ ![]() =
= ![]()
【解析】(1)先根据题意得出△BDE∽△CFD,再由相似三角形的性质即可得出结论;(2)①根据相似三角形的性质得到 ![]() ,推出△BDE∽△DEF,根据相似三角形的性质即可得到结论;②由四边形AEDF为菱形,得到∠AEF=∠DEF,于是得到∠AEF=60°,推出△ABC是等边三角形,△BED是等边三角形,得到BE=DE,即可得到结论.
,推出△BDE∽△DEF,根据相似三角形的性质即可得到结论;②由四边形AEDF为菱形,得到∠AEF=∠DEF,于是得到∠AEF=60°,推出△ABC是等边三角形,△BED是等边三角形,得到BE=DE,即可得到结论.

练习册系列答案
相关题目