Question

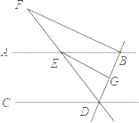
【题目】如图,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AB=21,AD=9.求AC的长.

Answer 1

【答案】17

【解析】试题分析：在AB上截取AE=AD，连接EC，作CF⊥AB于点F．可以得出△DAC≌△EAC，从而得到CE=CD=10=BC，利用等腰三角形“三线合一”的性质得到EF=FB=6，在Rt△BFC中和在Rt△AFC中，分别利用勾股定理即可得到结论．

试题解析：解：在AB上截取AE=AD，连接EC，作CF⊥AB于点F．

∵AC平分∠BAD，∴∠DAC=∠EAC．

在△DAC和△EAC中，∵AD=AE，∠DAC=∠EAC，AC=AC，∴△DAC≌△EAC（SAS），

∴CE=CD=10=BC，∴EF=FB=BE=（AB﹣AE）=（AB﹣AD）=6．

在Rt△BFC中，∵BC=10，FB=6，∴CF=8．

在Rt△AFC中，∵CF=8，AF=AE+EF=9+6=15，∴AC=17，∴AC的长为17．