题目内容
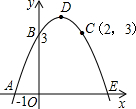
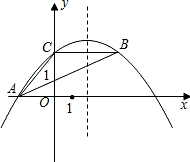
抛物线经过A、B、C三点,顶点为D,且与x轴的另一个交点为E.
(1)求该抛物线的解析式;
(2)求D和E的坐标,并求四边形ABDE的面积.
(1)求该抛物线的解析式;
(2)求D和E的坐标,并求四边形ABDE的面积.

(1)由图象得:
A点坐标为(-1,0),B点坐标为(0,3),C点坐标为(2,3),
代入y=ax2+bx+c得:
,
解得:
,
∴函数解析式为y=-x2+2x+3;
(2)∵函数解析式为y=-x2+2x+3,
∴y=-x2+2x+3,
=-(x2-2x)+3,
=-[(x2-2x+1)-1]+3,
=-(x-1)2+4,
所以顶点坐标为:D(1,4);
∵函数解析式为y=-x2+2x+3,与x轴的另一个交点为E,
顶点坐标为:D(1,4),可得出对称轴为x=1,A点坐标为(-1,0),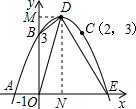
利用二次函数的对称性,可得出E点的坐标为(3,0),
连接AB,BD,DE,OD,做DM⊥OB,DN⊥OE,
四边形ABDE的面积:
s=△AOB+△BOD+△DOE,
=
AO×OB+
OB×MD+
OE×DN,
=
×1×3+
×3×1+
×3×4,
=9.
A点坐标为(-1,0),B点坐标为(0,3),C点坐标为(2,3),
代入y=ax2+bx+c得:
|
解得:
|
∴函数解析式为y=-x2+2x+3;
(2)∵函数解析式为y=-x2+2x+3,

∴y=-x2+2x+3,
=-(x2-2x)+3,
=-[(x2-2x+1)-1]+3,
=-(x-1)2+4,
所以顶点坐标为:D(1,4);
∵函数解析式为y=-x2+2x+3,与x轴的另一个交点为E,
顶点坐标为:D(1,4),可得出对称轴为x=1,A点坐标为(-1,0),

利用二次函数的对称性,可得出E点的坐标为(3,0),
连接AB,BD,DE,OD,做DM⊥OB,DN⊥OE,
四边形ABDE的面积:
s=△AOB+△BOD+△DOE,
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=9.

练习册系列答案
相关题目
 y轴的正半轴相交于点E,点B(-1,0),P是AC上的一个动点(P与点A、C不重合)
y轴的正半轴相交于点E,点B(-1,0),P是AC上的一个动点(P与点A、C不重合)
 段PC于E,且PD=PE.
段PC于E,且PD=PE.