题目内容
如图，点C是半圆O的半径OB上的动点，作PC⊥AB于C．点D是半圆上位于PC左侧的点，连接BD交线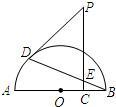
段PC于E，且PD=PE．
（1）求证：PD是⊙O的切线；
（2）若⊙O的半径为4
，PC=8
，设OC=x，PD2=y．
①求y关于x的函数关系式；
②当x=
时，求tanB的值．
段PC于E，且PD=PE．（1）求证：PD是⊙O的切线；
（2）若⊙O的半径为4
| 3 |
| 3 |
①求y关于x的函数关系式；
②当x=
| 3 |
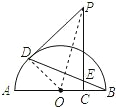
（1）证明：连接OD．
∵OB=OD，∴∠OBD=∠ODB．
∵PD=PE，∴∠PDE=∠PED．
∠PDO=∠PDE+∠ODE
=∠PED+∠OBD
=∠BEC+∠OBD
=90°，
∴PD⊥OD．
∴PD是⊙O的切线．
（2）①连接OP．
在Rt△POC中，
OP2=OC2+PC2=x2+192．
在Rt△PDO中，
PD2=OP2-OD2=x2+144．
∴y=x2+144（0≤x≤4
）．
（x取值范围不写不扣分）
②当x=
时，y=147，
∴PD=7
，（8分）
∴EC=
，
∵CB=3
，
∴在Rt△ECB中，tanB=
=
=
．
∵OB=OD，∴∠OBD=∠ODB．
∵PD=PE，∴∠PDE=∠PED．
∠PDO=∠PDE+∠ODE
=∠PED+∠OBD
=∠BEC+∠OBD
=90°，
∴PD⊥OD．
∴PD是⊙O的切线．
（2）①连接OP．
在Rt△POC中，
OP2=OC2+PC2=x2+192．
在Rt△PDO中，
PD2=OP2-OD2=x2+144．
∴y=x2+144（0≤x≤4
| 3 |
（x取值范围不写不扣分）
②当x=
| 3 |
∴PD=7
| 3 |
∴EC=
| 3 |
∵CB=3
| 3 |
∴在Rt△ECB中，tanB=
| CE |
| CB |
| ||
3
|
| 1 |
| 3 |
练习册系列答案
相关题目
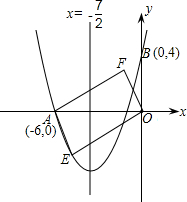
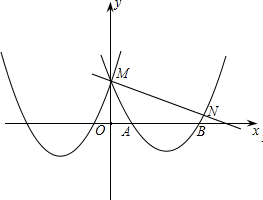点M，与x轴交于点A和B．
