Question

已知抛物线y=-

2

3

x2+bx+c与x轴交于不同的两点A（x₁，0）和B（x₂，0），与y轴交于点C，且x₁，x₂是方程x²-2x-3=0的两个根（x₁＜x₂）．
（1）求抛物线的解析式；
（2）过点A作AD∥CB交抛物线于点D，求四边形ACBD的面积；
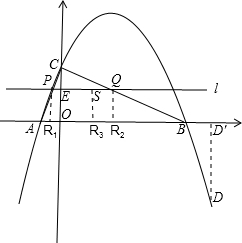
（3）如果P是线段AC上的一个动点（不与点A、C重合），过点P作平行于x轴的直线l交BC于点Q，那么在x轴上是否存在点R，使得△PQR为等腰直角三角形？若存在，求出点R的坐标；若不存在，请说明理由．

Answer 1

（1）解方程x²-2x-3=0，
得x₁=-1，x₂=3．
∴点A（-1，0），点B（3，0）．
∴

- 2 3 ×(-1)2+b•(-1)+c=0 - 2 3 ×32+b•3+c=0

，
解，得

b= 4 3 c=2

，
∴抛物线的解析式为y=-

2

3

x²+

4

3

x+2．

（2）∵抛物线与y轴交于点C．
∴点C的坐标为（0，2）．
又点B（3，0），可求直线BC的解析式为y=-

2

3

x+2．
∵AD∥CB，
∴设直线AD的解析式为y=-

2

3

x+b′．
又点A（-1，0），
∴b′=-

2

3

，直线AD的解析式为y=-

2

3

x-

2

3

．
解

y=- 2 3 x2+ 4 3 x+2 y=- 2 3 x- 2 3

，
得

x1=-1 y1=0

，

x2=4 y2=- 10 3

，
∴点D的坐标为（4，-

10

3

）．
过点D作DD’⊥x轴于D’，DD’=

10

3

，则又AB=4．
∴四边形ACBD的面积S=

1

2

AB•OC+

1

2

AB•DD’=10

2

3

．

（3）假设存在满足条件的点R，设直线l交y轴于点E（0，m），
∵点P不与点A、C重合，
∴0＜m＜2，
∵点A（-1，0），点C（0，2），
∴可求直线AC的解析式为y=2x+2，
∴点P（

1

2

m-1，m）．
∵直线BC的解析式为y=-

2

3

x+2，
∴点Q（-

3

2

m+3，m）．
∴PQ=-2m+4．在△PQR中，
①当RQ为底时，过点P作PR₁⊥x轴于点R₁，则∠R₁PQ=90°，PQ=PR₁=m．
∴-2m+4=m，
解得m=

4

3

，
∴点P（-

1

3

，

4

3

），
∴点R₁坐标为（-

1

3

，0）．
②当RP为底时，过点Q作QR₂⊥x轴于点R₂，
同理可求，点R₂坐标为（1，0）．
③当PQ为底时，取PQ中点S，过S作SR₃⊥PQ交x轴于点R₃，
则PR₃=QR₃，∠PR₃Q=90度．
∴PQ=2R₃S=2m．
∴-2m+4=2m，
解，得m=1，
∴点P（-

1

2

，1），点Q（

3

2

，1），可求点R₃坐标为（

1

2

，0）．
经检验，点R₁，点R₂，点R₃都满足条件．
综上所述，存在满足条件的点R，它们分别是R₁（-

1

3

，0），R₂（1，0）和点R₃（

1

2

，0）．