题目内容
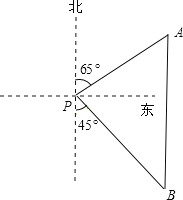
【题目】如图，一艘海轮位于灯塔P的北偏东65°方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，这时，海轮所在的B处距离灯塔P有多远？（结果用非特殊角的三角函数及根式表示即可）
【答案】80
cos25°
【解析】
首先根据题意得出∠MPA=∠A=65°，以及∠DBP=∠DPB=45°，在Rt△PAD中利用三角函数求出PD的长，再在Rt△PBD中利用解直角三角形求出PB即可．
解：过点P作PD⊥AB于点D，
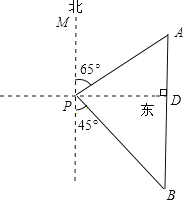
∵点A在P的北偏东65°方向，
∴∠APD＝25°，
在Rt△PAD中，
cos25°＝
，
∴PD＝PAcos25°＝80cos25°．
由题意知∠DPB＝45°，
在Rt△PBD中，cos45°＝
，
∴PB＝PD.
∴PB＝80cos25°．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
