Question

【题目】已知四边形ABCD中，E，F分别是AB，AD边上的点，DE与CF交于点G.

(1)如图①，若四边形ABCD是矩形，且DE⊥CF，求证： ；

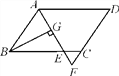
(2)如图②，若四边形ABCD是平行四边形，试探究：当∠B与∠EGC满足什么关系时，使得成立？并证明你的结论．

Answer 1

【答案】（1）详见解析；（2）当∠B＋∠EGC＝180°时，成立，理由详见解析.

【解析】

(1)根据矩形的性质可得∠A＝∠ADC＝90°，由DE⊥CF可得∠ADE＝∠DCF，即可证得△ADE∽△DCF，从而证得结论；

(2)在AD的延长线上取点M，使CM＝CF，则∠CMF＝∠CFM．根据平行线的性质可得∠A＝∠CDM，再结合∠B+∠EGC＝180°，可得∠AED＝∠FCB，进而得出∠CMF＝∠AED即可证得△ADE∽△DCM，从而证得结论；

解：(1)∵四边形ABCD是矩形，∴∠A＝∠ADC＝90°，

∵DE⊥CF，∴∠ADE＝∠DCF，

∴△ADE∽△DCF，

∴ 　

(2)当∠B＋∠EGC＝180°时，成立，证明如下：

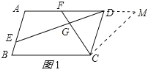
在AD的延长线上取点M，使CM＝CF，

则∠CMF＝∠CFM.

∵AB∥CD.∴∠A＝∠CDM.

∵AD∥BC，∴∠CFM＝∠FCB.

∵∠B＋∠EGC＝180°，∴∠AED＝∠FCB，

∴∠CMF＝∠AED，∴△ADE∽△DCM，∴，即.